【問題】
ピアノでド、レ、ミ、ファ、ソ、ファ、ミ、レ、ド、レ、ミ…と繰り返し弾く。
（1）18番目に弾く音は何か求めなさい。
（2）1回目のミを弾くのは3番目、2回目のミを弾くのは7番目です。8回目のミを弾くのは何番目か求めなさい。
（3）n回目のミを弾くのは何番目か。nを用いて表しなさい。
答え
（1）レ
（2）31番目
（3）4n-1 番目
（1）
今回のように、同じ動作を何回も繰り返していく場合には、
1つの周期に注目してみるといいでしょう。
今回であれば、
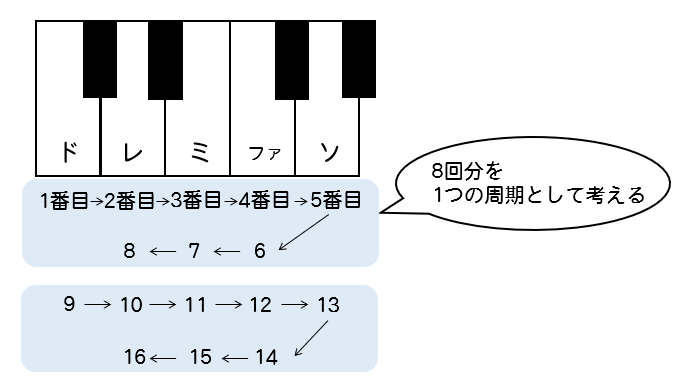
ド → レ → … → レ までの8回分を1つの周期として考えていくといいです。
問題で与えられている画像を見ると、
ド→…→ドまで含めて1周期としたくなりますが、
そうすると上手くサイクルしていかないので注意ですね(^^;)
すると、18番目というのは
2周分（16回）＋2番目ということがわかります。
よって、18番目は『レ』となります。
こうやって周期を考えていくと、
100番目は？？
と問われても次のように簡単に求まりますね。
100の中に8回分が何個入るかを考えると…
100\div 8=12…4 となり、12周と4番目ということがわかります。
よって、答えは『ファ』となりますね。
（2）
『ミ』が出てくる周期を考えてみると、
3 → 7 → 11 → 15 …
と、3から始まり4ずつ増えている等差数列であることに気が付きます。
となると、話は早いですね。
8番目は、最初の3に4を7回分加えた値になるので
3+4\times 7=31番目
となります。
等差数列の考え方を忘れてしまった方はこちらで復習！
⇒ 規則性の問題をやる上で覚えておきたい公式
（3）
n番目のときも先ほどと同じように考えましょう。
n番目は、最初の3に4を(n-1)回分加えた値になるので
3+4\times (n-1)=4n-1 番目
となります。