【問題】
関数y=ax^2 のグラフについて、次の問いに答えなさい。
（1）xの値が2から4まで増加するときの変化の割合が3である。このとき、aの値を求めなさい。
（2）xの変域が-2≦x≦3 のとき、yの変域は0≦y≦18 である。このとき、aの値を求めなさい。
（3）下の図は、a=3のときのグラフである。このグラフ上に2点A、Bがあり、点A、Bのy 座標はともに3である。△ABCの面積が、△OABの面積の3倍となるグラフ上の点Cは2つある。その点の座標を求めなさい。
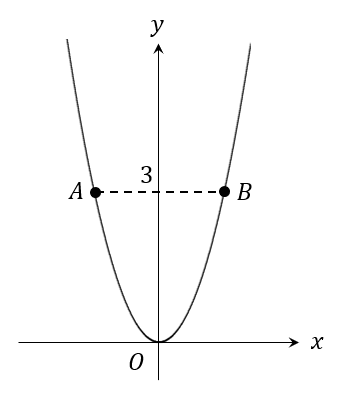
答え
（1）a=\frac{1}{2}
（2）a=2
（3）(-2,12),(2,12)
（1）
関数y=ax^2 については、
裏ワザ公式を用いて変化の割合を求めると楽勝です。
すると、y=ax^2が2から4まで増加するときの変化の割合は、
a(2+4)=6a
と表すことができます。
これが3になるということなので、
\begin{eqnarray}6a&=&3\\[5pt]a&=&\frac{1}{2}\end{eqnarray}
となります。
（2）
変域から式を求める場合には、
次のようにグラフのイメージを書いて座標を読み取りましょう。
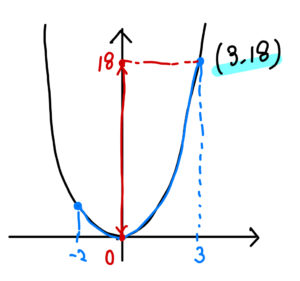
すると、(3,18) を通ることが分かるので、y=ax^2に代入して計算していきましょう。
\begin{eqnarray}18&=&a\times 3^2\\[5pt]9a&=&18\\[5pt]a&=&2\end{eqnarray}
（3）
まずは、△OABの面積を考えてみましょう。
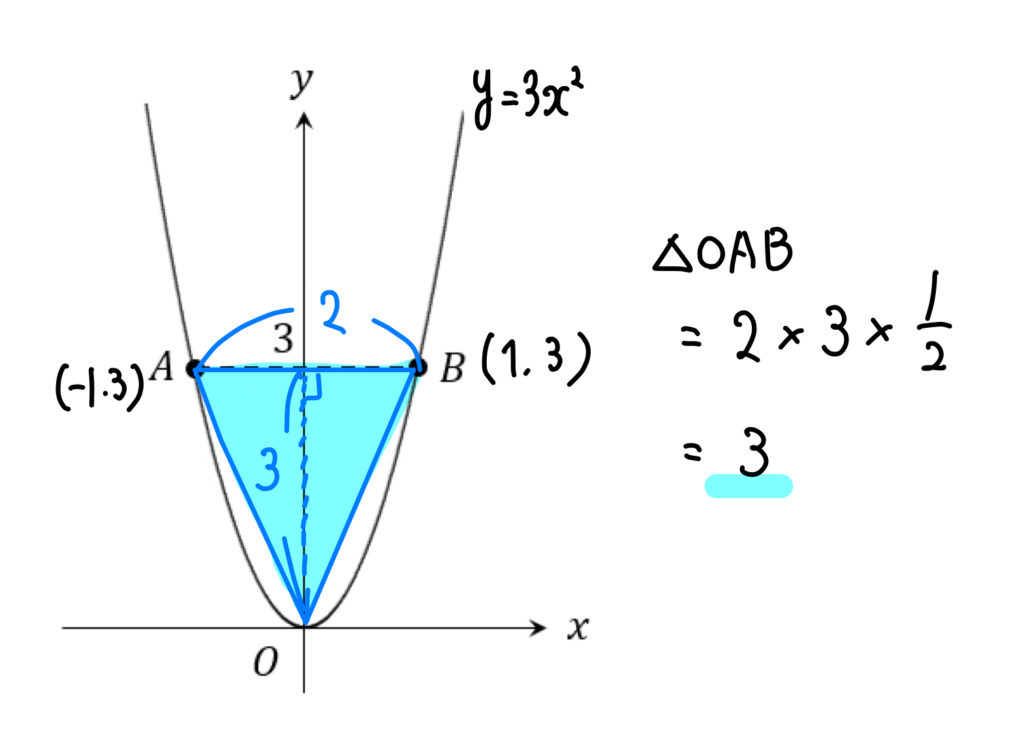
すると、△OABの面積は3であると分かりました。
よって、△ABCの面積は9になります。
辺ABを底辺と考えると、AB=2より
高さは9になる必要があります。
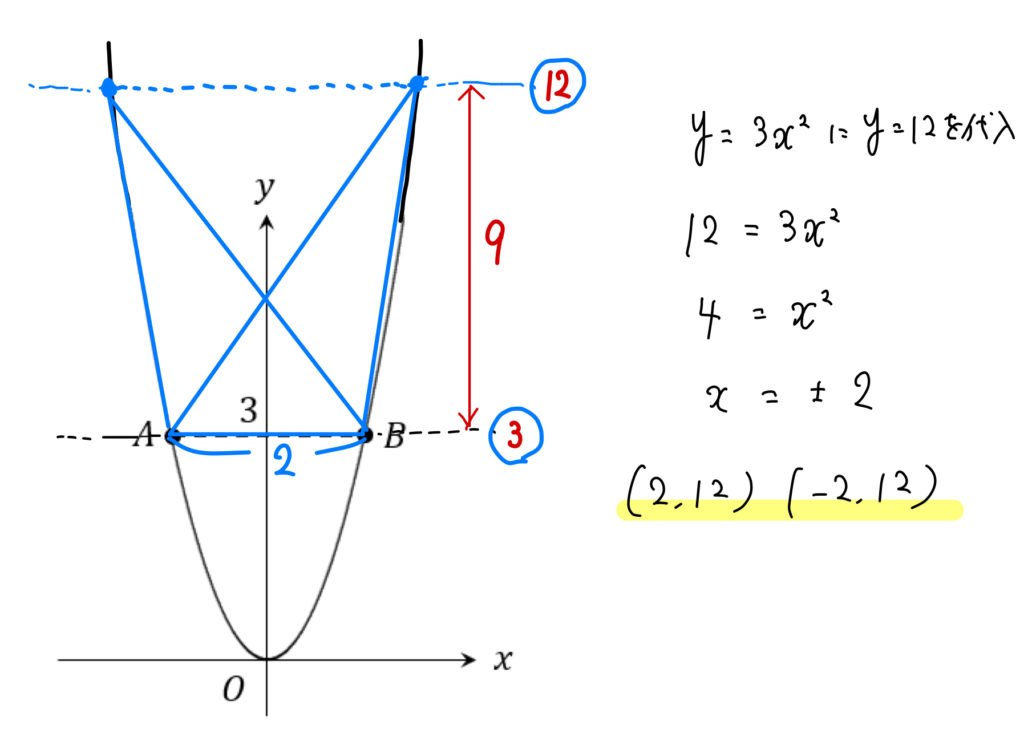
なので、点Cのy座標は3+9=12となります。
y座標が求まれば、y=3x^2に代入して
x座標を求めることができますね。
よって、点Cの座標は(2,12),(-2,12) となります。