【群馬16】関数の入試問題（★☆☆）

【問題】

下の図において、放物線アは関数 $y=\frac{1}{2}x^2$ のグラフで、放物線ア上にある2点A、Bは、 $x$ 座標がそれぞれ $-2$ 、 $4$ である。また、双曲線イは点Aを通る反比例のグラフで、点Cは、点Bを通り $y$ 軸に平行な直線と双曲線イとの交点である。

（1）Aの $y$ 座標を求めなさい。

（2）双曲線イのグラフについて、 $y$ を $x$ の式で表しなさい。

（3）三角形ABCの面積を求めなさい。

解答

答え

（1） $2$

（2） $y=-\frac{4}{x}$

（3） $27$

解説

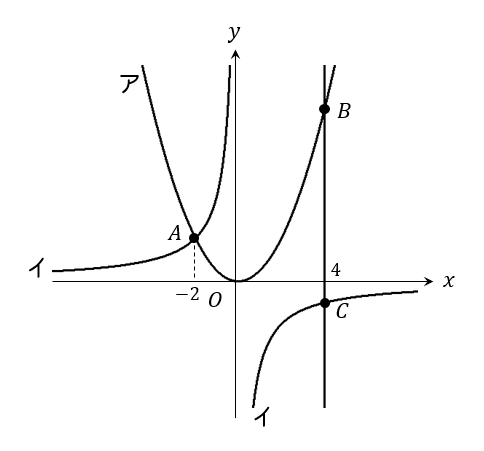
（1）

$x=-2$ を $y=\frac{1}{2}x^2$ に代入すると、 $y$ 座標が求まります。

$\begin{eqnarray}y&=&\frac{1}{2}\times (-2)^2\\[5pt]&=&\frac{1}{2}\times 4\\[5pt]&=&2\end{eqnarray}$

（2）

（1）より、Aの座標が $(-2,2)$ であることが分かりました。

これは双曲線イ上の点でもあるので、

式を作るのに用いることができます。

よって、双曲線(反比例)の式である $y=\frac{a}{x}$ に $x=-2$ 、 $y=2$ を代入すると

$\begin{eqnarray}2&=&\frac{a}{-2}\\[5pt]-4&=&a\end{eqnarray}$

よって、式は $y=-\frac{4}{x}$ となります。

（3）

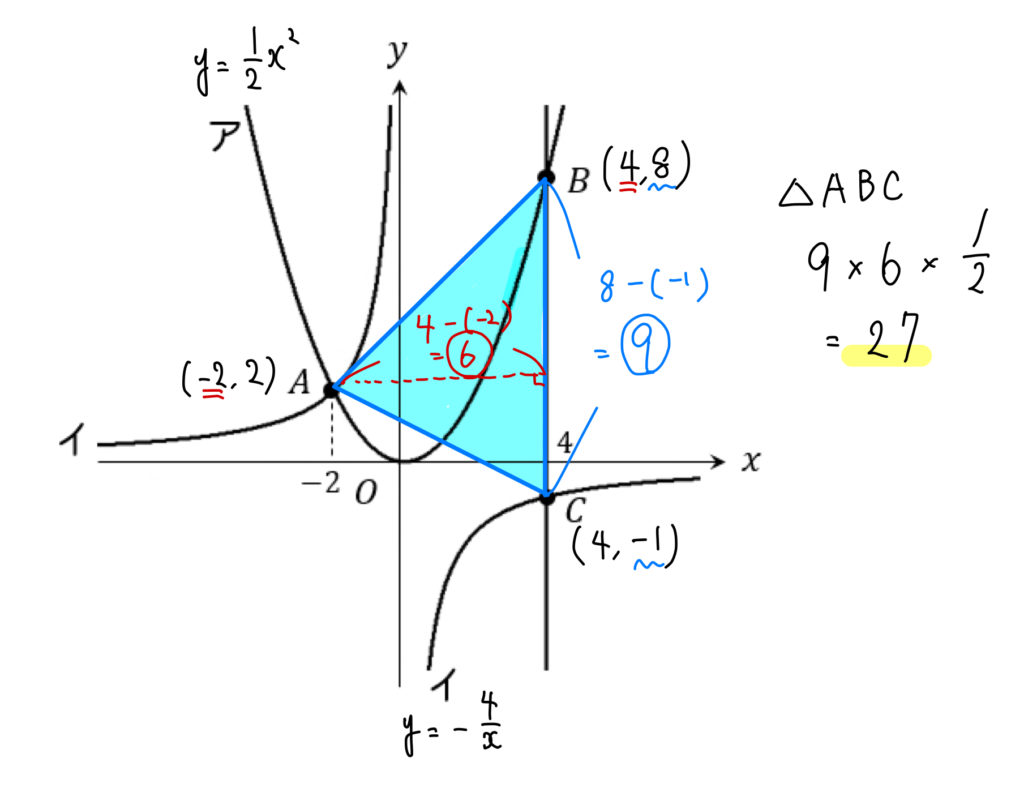
グラフ上の図形の面積を求めるには、

各頂点の座標を求めるのが基本となります。

点Bは $y=\frac{1}{2}x^2$ に $x=4$ を代入すると、

$y=\frac{1}{2}\times 4^2=8$ ⇒ $A(4,8)$

点Cは $y=-\frac{4}{x}$ に $x=4$ を代入すると、

$y=-\frac{4}{4}=-1$ ⇒ $C(4,-1)$

それぞれの $y$ 座標を求めることができます。

よって、面積は次のように計算ができます。