【問題】
下の図において、①は関数y=x^2 、②は関数y=-\frac{1}{2}x^2 のグラフである。点Aは①のグラフ上を動き、異なる2点B、Cは②のグラフ上を動く。2点A、Cはx 座標が等しく、2点B、Cはy 座標が等しい。また、線分AB、ACとx 軸との交点をそれぞれD、Eとする。ただし、点Aのx 座標は正とする。
（1）点Aのx 座標が4のとき、点Cの座標を求めなさい。
（2）△ADEと△ABCの面積の比を、最も簡単な整数の比で表しなさい。
（3）点Aのx 座標を2とする。3点A、B、Cを通る円とx 軸との交点のうち、x 座標が正の点をPとするとき、点Pのx 座標を求めなさい。
答え
（1）(4,-8)
（2）4:9
（3）2\sqrt{3}
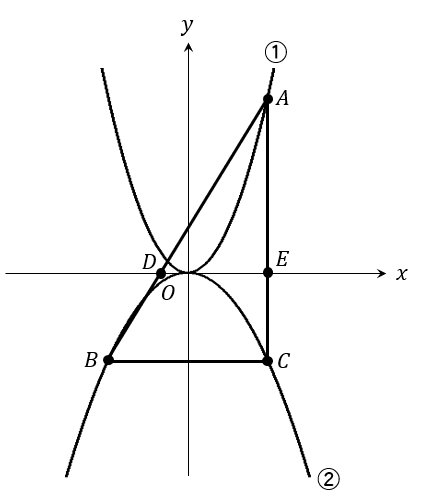
（1）
点Cのx 座標は4だから、
②の関数であるy=-\frac{1}{2}x^2 に代入するとy 座標が求まります。
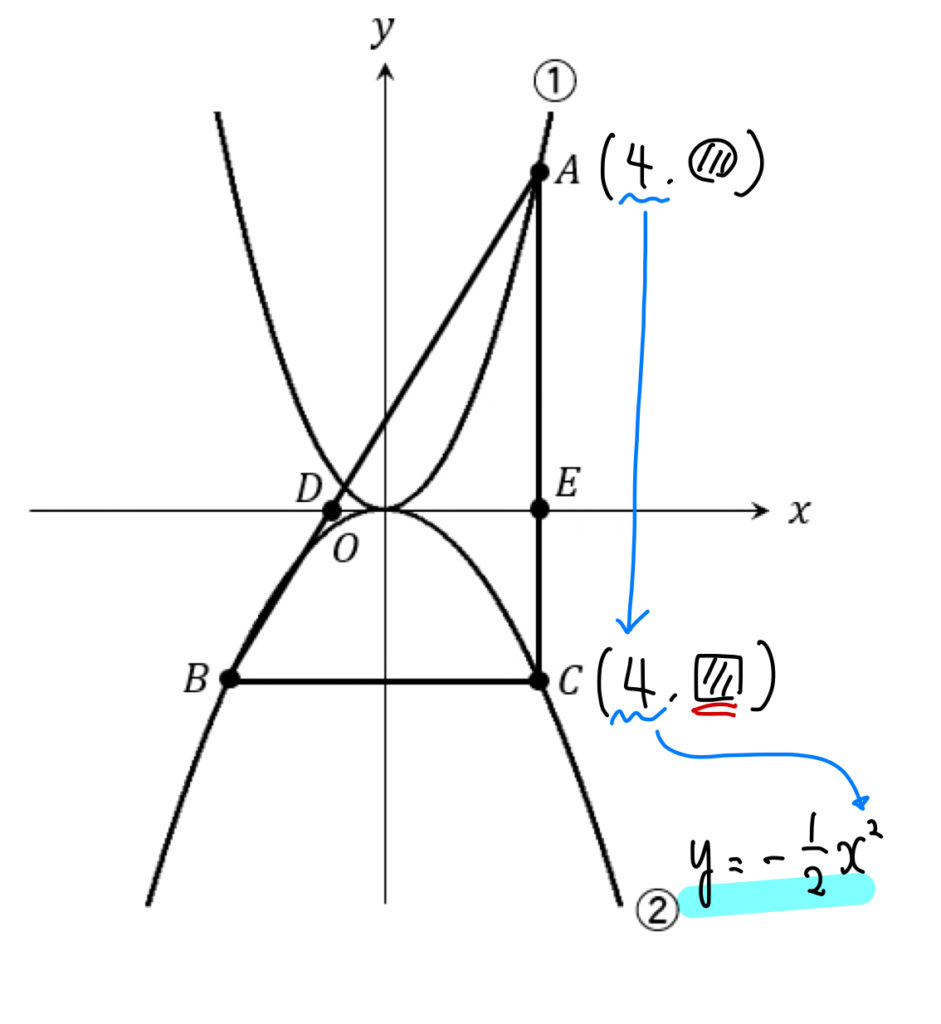
\begin{eqnarray}y&=&-\frac{1}{2}\times 4^2\\[5pt]&=&-8\end{eqnarray}
（2）
△ADEと△ABCは相似な関係になっています。
なので、相似比を二乗することで面積比が求まります。
- 座標を文字で置く
- 長さを表す
- 相似比を求める
- 面積比を求める
この手順で進めていきましょう。
まず、点Aのx 座標をa とすると、
点A(a,a^2)、点E(a,0)、点C\left(a,-\frac{1}{2}a^2\right)
と表すことができます。
そこから辺の長さを求めて、相似比を考えると
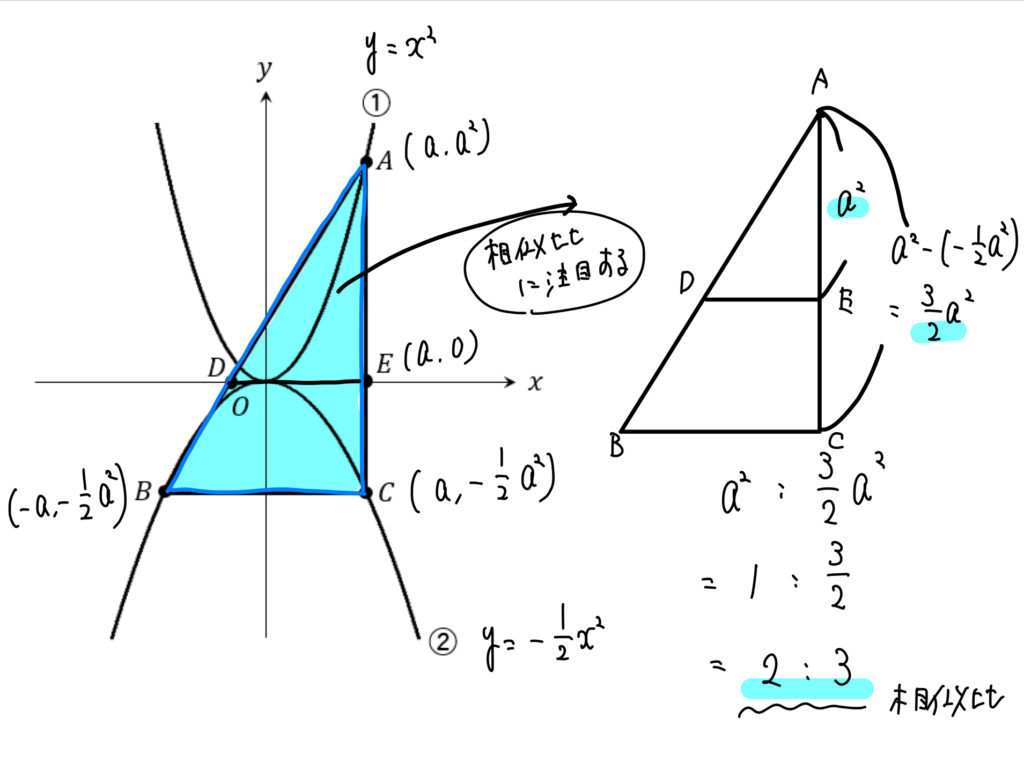
△ADEと△ABCの相似比は、2:3 であることが分かりました。
よって、△ADEと△ABCの面積比は、
相似比を2乗したものになるので、4:9となります。
（3）
∠ACB＝90°であることから、
円周角の定理より、∠APBも同じく90°になることが分かります。
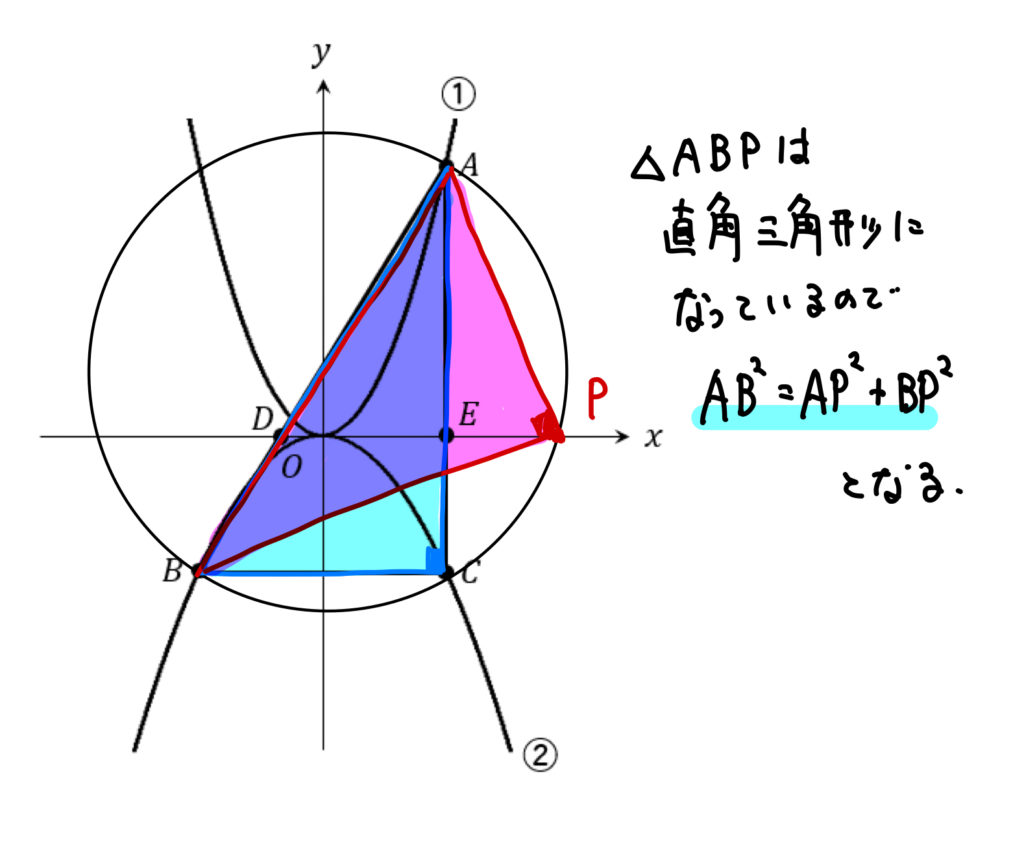
よって、△ABPが直角三角形であることから
三平方の定理を用いて、点Pの座標を求めていきます。
点Pのx 座標をa とすると、
AB^2、AP^2、BP^2は次のように表せます。
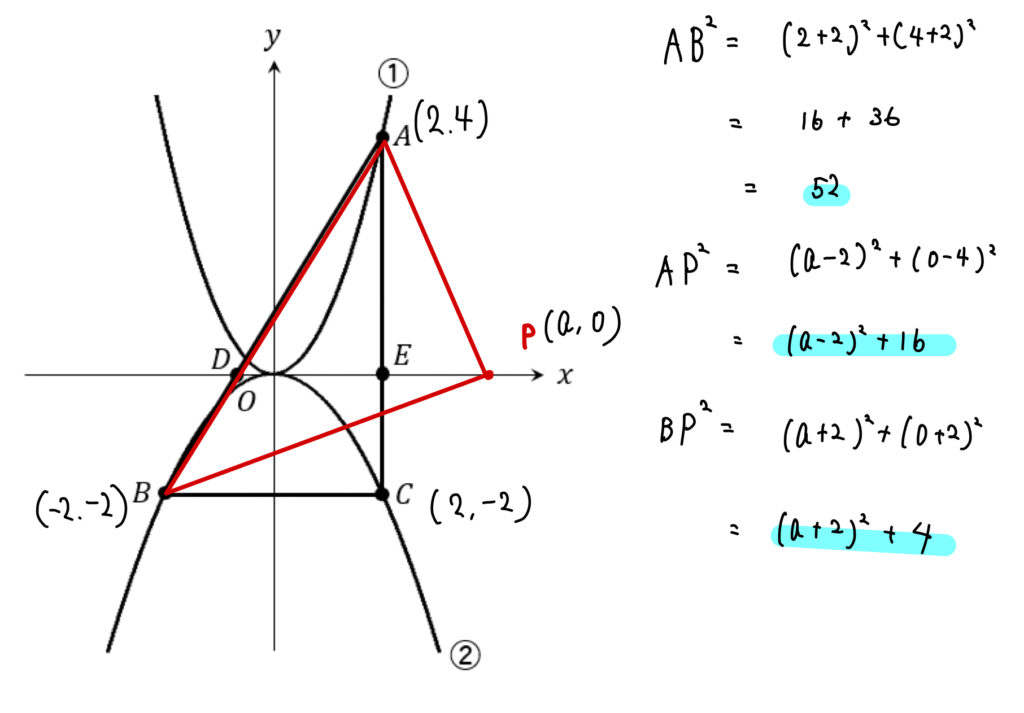
これらを三平方の定理、AB^2=AP^2+BP^2に当てはめると
\begin{eqnarray}52&=&(a-2)^2+16+(a+2)^2+4\\[5pt]52&=&a^2-4a+4+16+a^2+4a+4+4\\[5pt]0&=&2a^2-24\\[5pt]2a^2&=&24\\[5pt]a^2&=&12\\[5pt]a&=&\pm2\sqrt{3}\end{eqnarray}
問題文より、点Pのx座標は正であるといっているので、2\sqrt{3} となります。