【問題】
図では、Oは原点、点A、Bの座標はそれぞれ\((3,4)\)、\((6,2)\)である。
（1）直線ABの式を求めなさい。
（2）直線\(y=x+b\) (\(b\)は定数) が線分AB上の点を通るとき、\(b\)がとることのできる値の範囲を求めなさい。
解答
答え
（1）\(y=-\frac{2}{3}x+6\)
（2）\(-4≦b≦1\)
解説
（1）
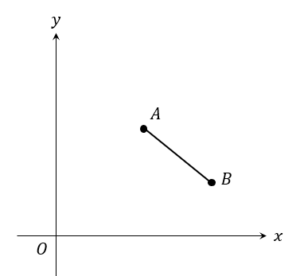
2点\((3,4)\)、\((6,2)\)を\(y=ax+b\) に当てはめて計算していきましょう。
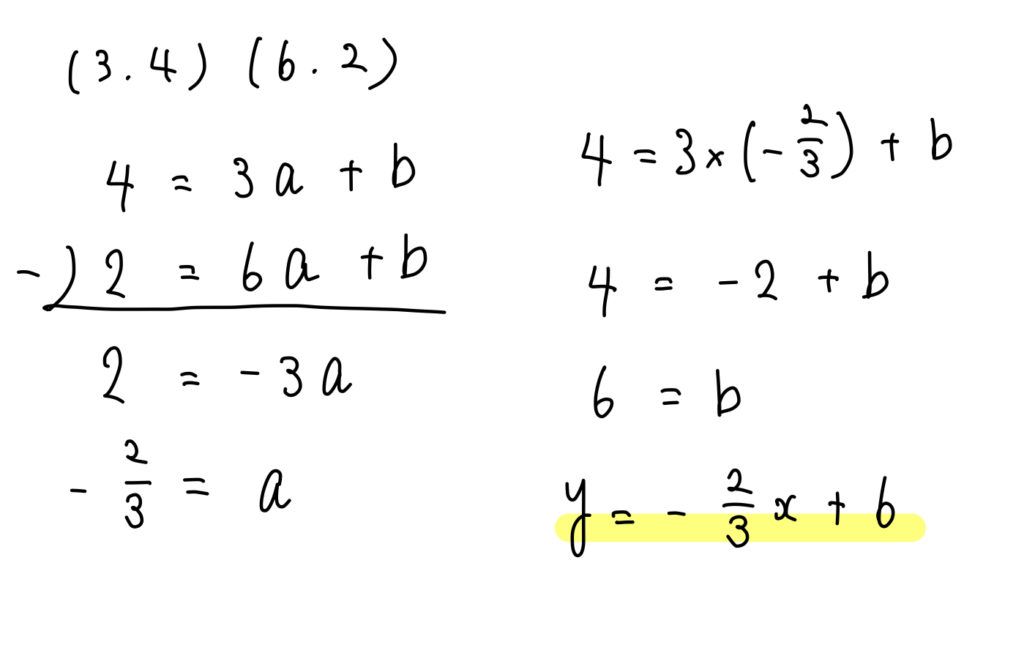
（2）
直線\(y=x+b\)における、\(b\)の範囲とは、
言いかえると、切片の範囲のことです。
\(y=x+b\)(傾き1)の直線を、
線分ABを通るように引くと
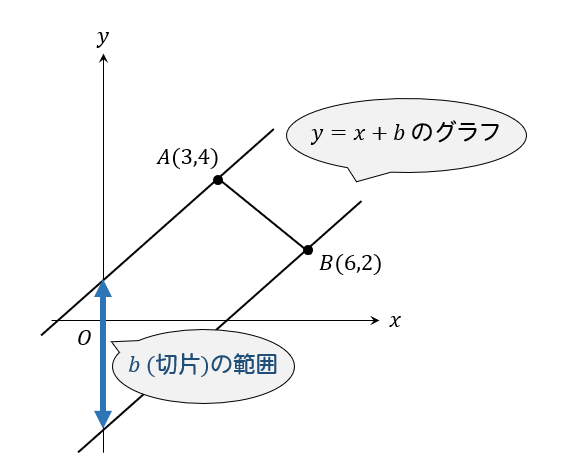
\(b\)（切片）の範囲はこのようになっています。
つまり、点Aを通ったときが一番\(b\)が大きく、
点Bを通ったときが一番\(b\)が小さくなります。
点A\((3,4)\)を通るときは、
$$\begin{eqnarray}4&=&3+b\\[5pt]1&=&b\end{eqnarray}$$
点B\((6,2)\)を通るときは、
$$\begin{eqnarray}2&=&6+b\\[5pt]-4&=&b\end{eqnarray}$$
よって、\(b\)の範囲は \(-4≦b≦1\) となります。