【問題】
下の図のように、関数y=\frac{1}{8}x^2 のグラフ上に2点A、Bがあり、2点A、Bのx 座標はそれぞれ-8、4である。2点A、Bを通る直線とy 軸との交点をC、x軸との交点をDとする。また、x軸上に∠ACE=90° となるように点Eをとる。
（1）2点A、Bを通る直線の式を求めよ。
（2）点Dの座標を求めよ。また、線分DEの長さを求めよ。
答え
（1）y=-\frac{1}{2}x+4
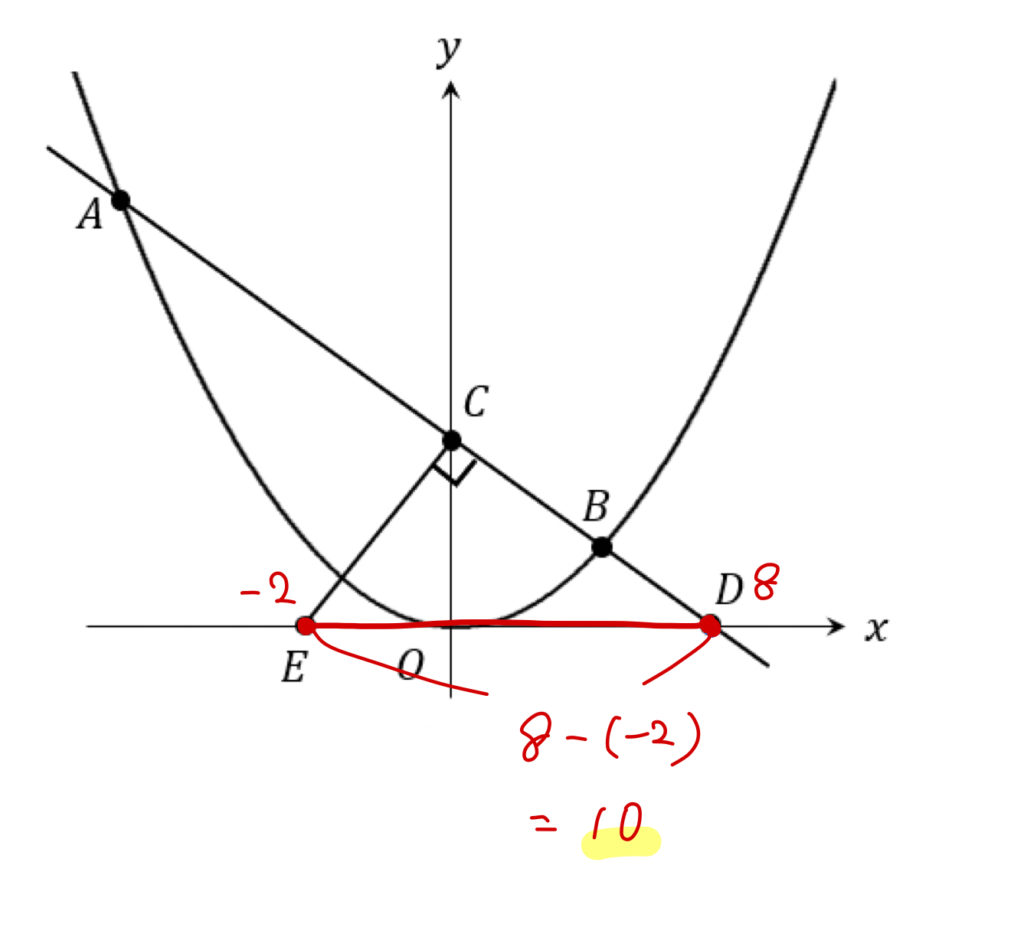
（2）D(8,0)、DE=10
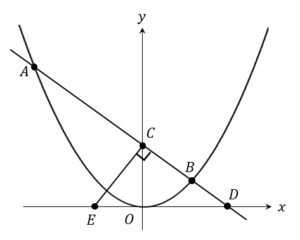
（1）
まずは2点A、Bの座標を求めましょう。
点Aのx 座標は-8なので、
y=\frac{1}{8}\times (-8)^2=8
よって、点A(-8,8)
点Bのx 座標は4なので、
y=\frac{1}{8}\times 4^2=2
よって、点B(4,2)
2点(-8,8)、(4,2)をy=ax+b に当てはめて計算していきましょう。
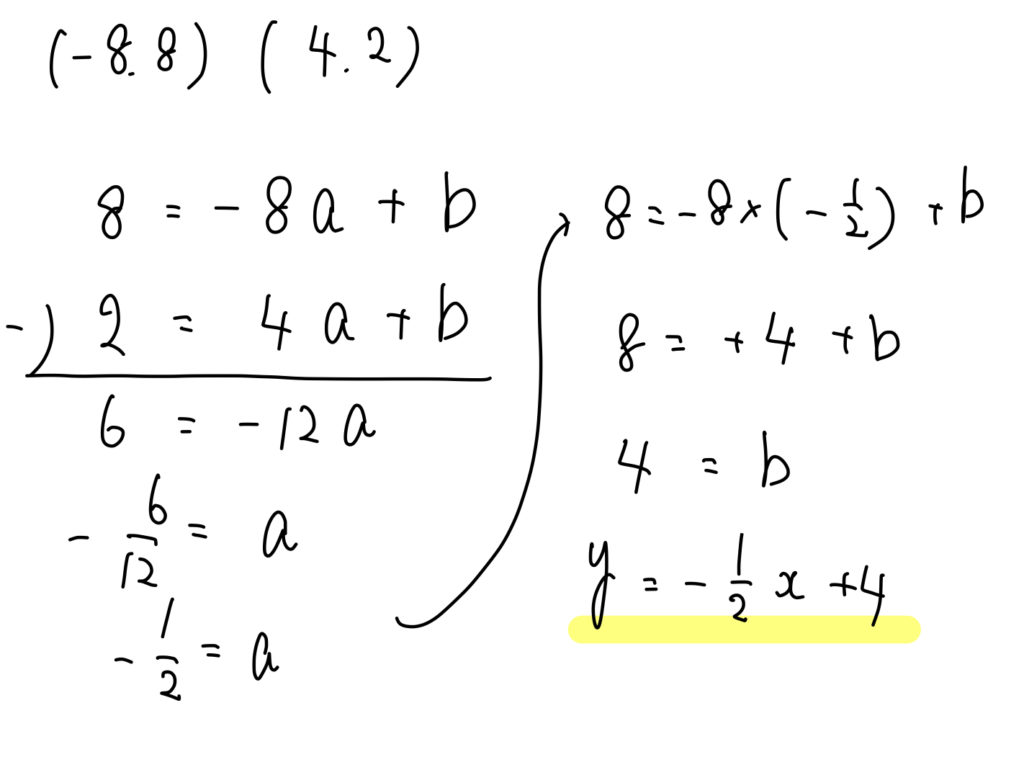
（2）
点Dは、y=-\frac{1}{2}x+4 にy=0 を代入するとx 座標を求めることができます。
\begin{eqnarray}0&=&-\frac{1}{2}x+4\\[5pt]\frac{1}{2}x&=&4\\[5pt]x&=&8\end{eqnarray}
よって、点Dの座標は(8,0) となります。
次に線分DEの長さを求めるため
点Eの座標を求めていきます。
直線CEは、直線ABと垂直な関係です。
なので、互いの傾きを掛けると-1になります。
垂直な直線は、互いの傾きを掛けると-1になる。
というわけで、直線ECの傾きをa とすると、
\begin{eqnarray}a\times \left(-\frac{1}{2}\right)&=&-1\\[5pt]a&=&2\end{eqnarray}
a=2 となります。
よって、直線ECの式は y=2x+4。
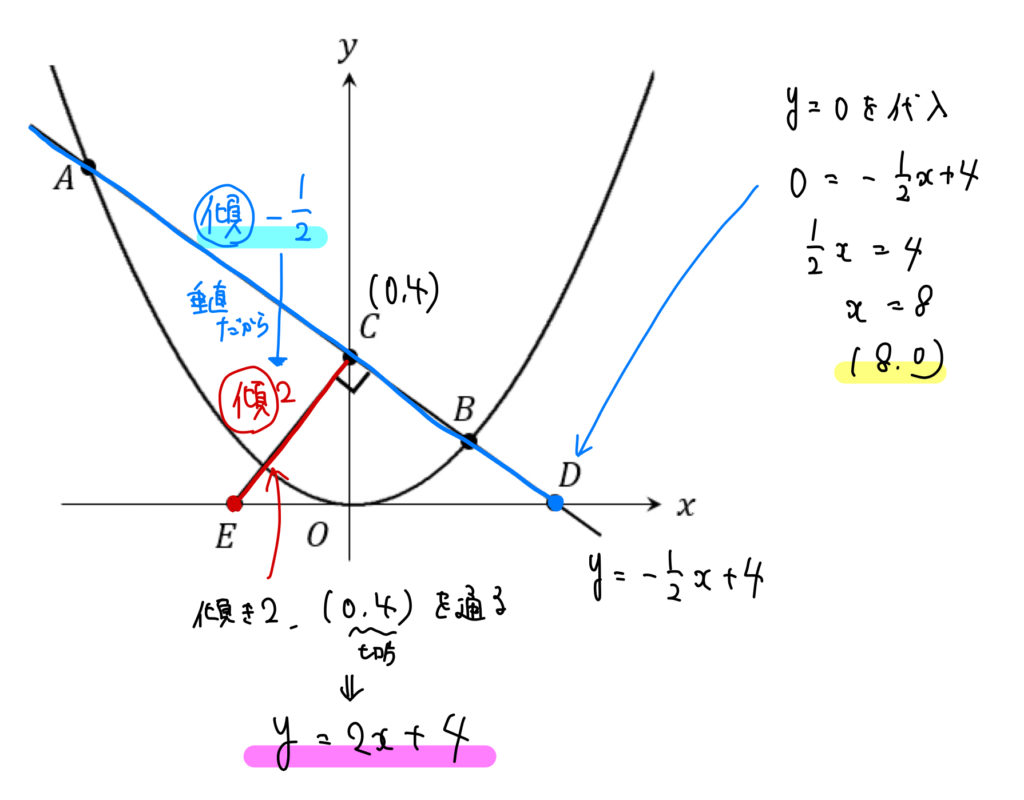
さらに、x 軸との交点である点Dの座標は、
\begin{eqnarray}0&=&2x+4\\[5pt]-2x&=&4\\[5pt]x&=&-2\end{eqnarray}
点D(-2,0) と求まりました。
よって、線分DEの長さは
8-(-2)=10
となりました。
