【問題】
下の図のように、3点A(6,5)、B(-2,3)、C(2,1)を頂点とする△ABCがある。
（1）△ABCの面積を求めなさい。
（2）点Aを通り、直線BCに平行な直線の式を求めなさい。
（3）直線OC上に点Pをとり、△OPBと四角形OCABの面積が等しくなるようにする。このとき、点Pの座標を求めなさい。ただし、点Pのx 座標は正とする。
解答
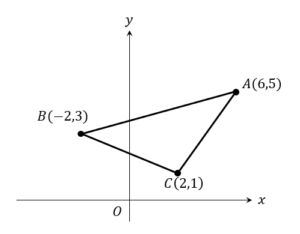
答え
（1）12
（2）y=-\frac{1}{2}x+8
（3）(8,4)
解説
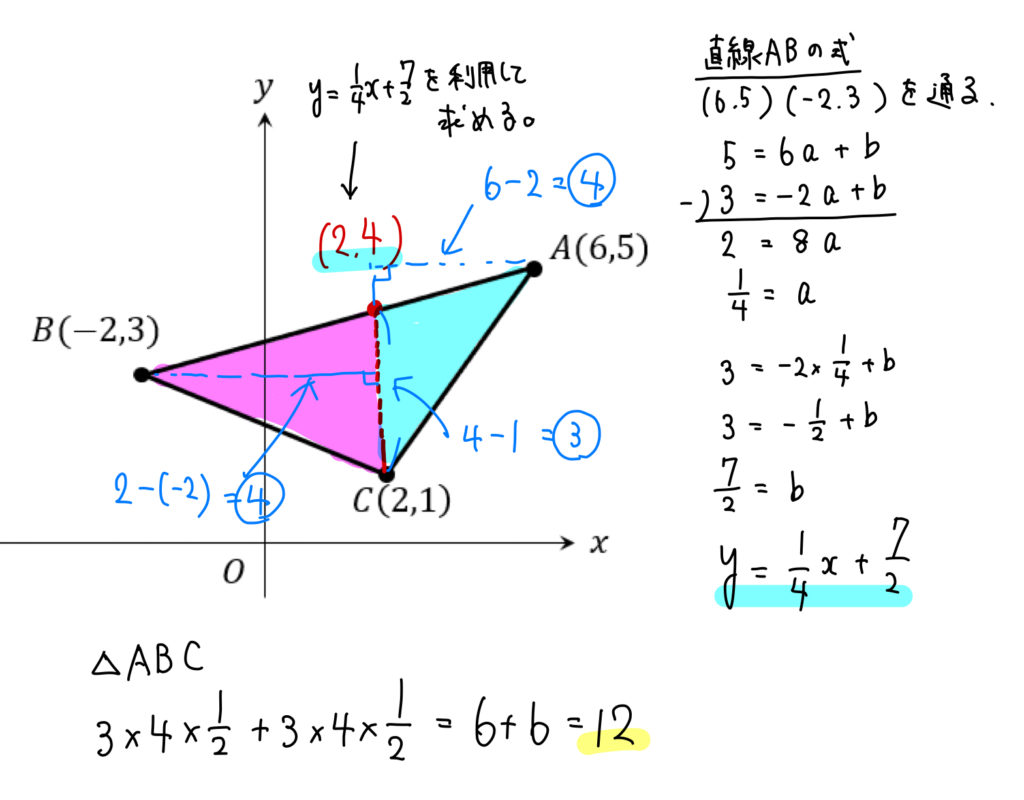
（1）
直線ABの式を求める ⇒ 三角形を分割する ⇒ 面積を求める
この手順で攻めていきましょう！
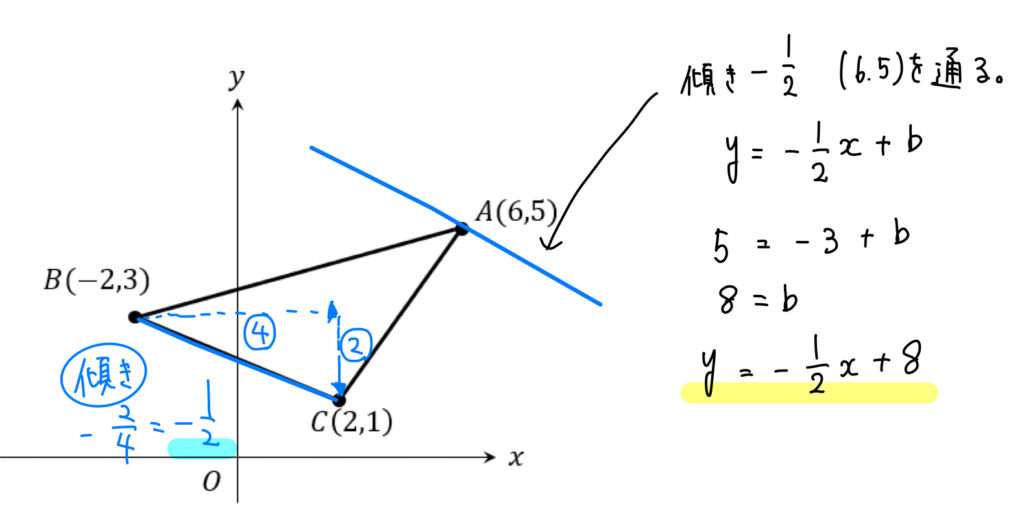
（2）
「平行な直線 ＝ 傾きが等しい」 ですね。
（3）
等積変形の考え方を利用して解いていきましょう。
ここでは（2）の問題が布石となっています。
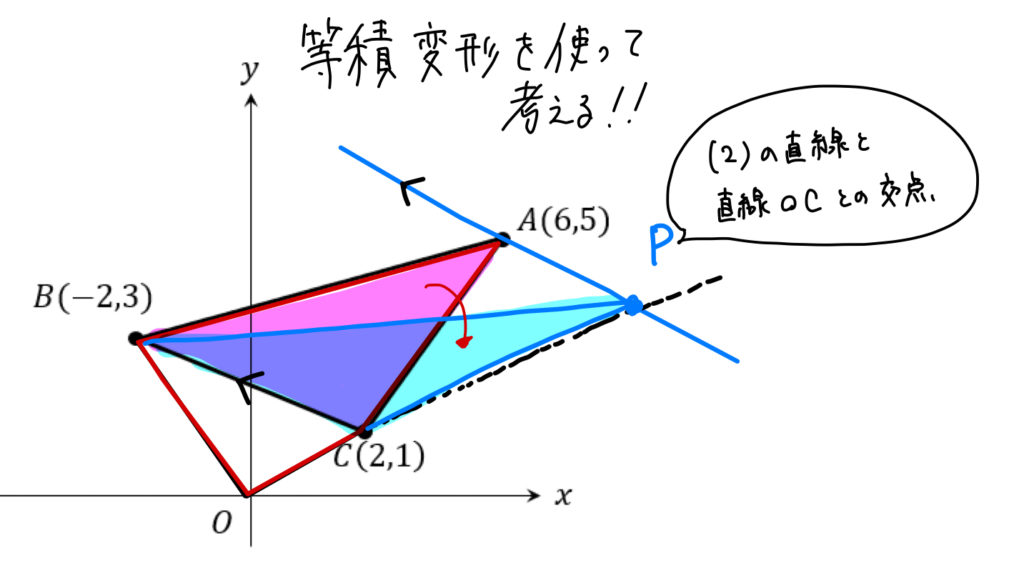
このように、直線OC上に点Pをとり
等積変形をすることで、
四角形OCABと面積の等しい△OPBを作ることができます。
というわけで、
直線OC(y=\frac{1}{2}x)と、直線y=-\frac{1}{2}x+8 の交点を求めます。
それぞれを連立方程式で解けばよいので、
\begin{eqnarray}\frac{1}{2}x&=&-\frac{1}{2}x+8\\[5pt]x&=&-x+16\\[5pt]2x&=&16\\[5pt]x&=&8\end{eqnarray}
x=8 をy=\frac{1}{2}x に代入すると、
y=\frac{1}{2}\times 8=4
よって、点P(8,4) となります。