こんにちは、数スタの小田です。
関数メルマガ講座を受講してくれて、ありがとうございます(^^)
この講座では、あなたの力を劇的にアップさせる関数のコツをお伝えしていきます。
各講座の内容は非常に濃いです。
なので、全部をこなすまでには時間がかかると思いますが、
1つずつゆっくりで構いませんので、確実にこなしていってください。
この講座で紹介する講義をすべて受講すれば、
これまでは全く解けなかったような問題がスラスラと解けるようになりますよ(^^)
そして!
毎回の講義を受講し終えたら、記事下のコメントフォームからコメントをしてください!
コメントをくれた方には、追加の特別講義をプレゼントしています。
こちらのプレゼント講義も関数の得点アップには欠かせないものですので、
必ず受け取るようにしてくださいね!
関数メルマガ講座の第1回目は、
「文字座標のコツ」についてです。
今回の講義を通して、
次のような問題が解けるようになってもらいます。
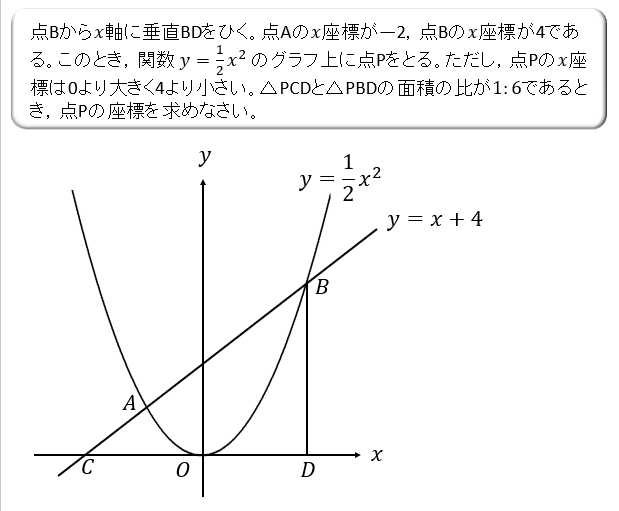
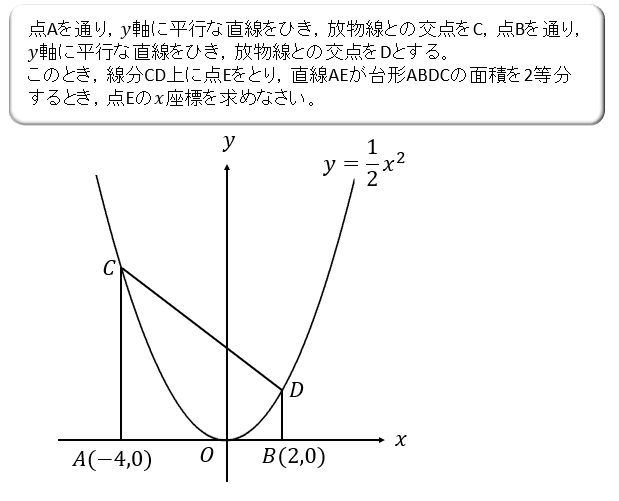
このような文字座標を扱う問題では、
次のステップで基礎を固めておくと理解度がアップします。
【文字座標の攻略ステップ】
- 座標の求め方を理解する
- ①を利用して長さの求め方を理解する
- 文字座標の応用に挑戦する
というわけで、
このステップにそって講義を公開していくので、
上から順に受講していきましょう!
【1】座標の求め方
【動画講義】座標の求め方
(動画時間:23分18秒)
座標の求め方の基本
軸との交点
\(x\)軸との交点を求めたい場合には、関数の式に\( y=0 \)を代入して求めましょう。
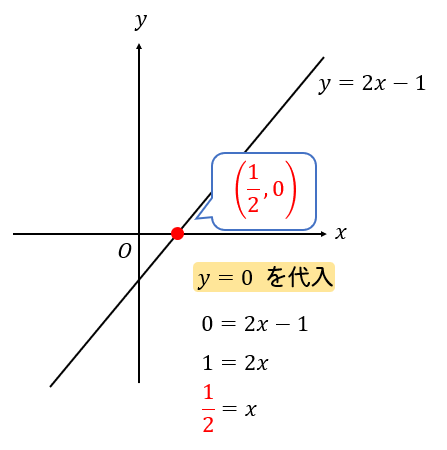
\(y\)軸との交点を求めたい場合には、関数の式に\( x=0 \)を代入して求めましょう。
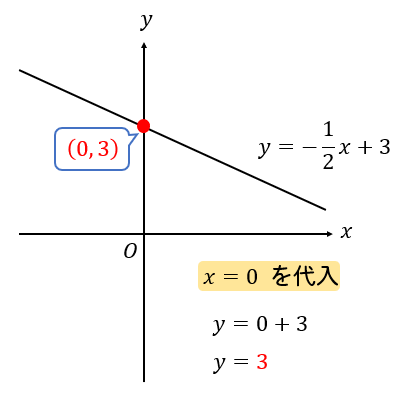
切片を見れば一発でわかりますけどね!
グラフ上の点
\(x\)座標が分かっている場合には、関数の式に \(x\)の値を代入して\(y\)座標を求めます。
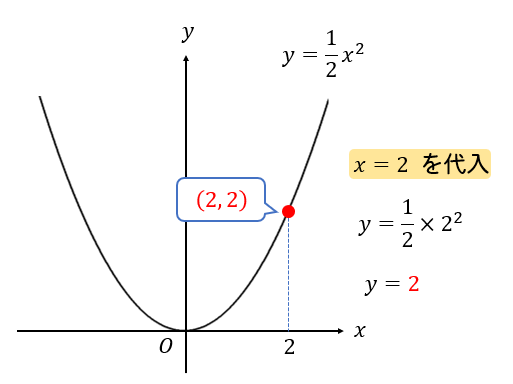
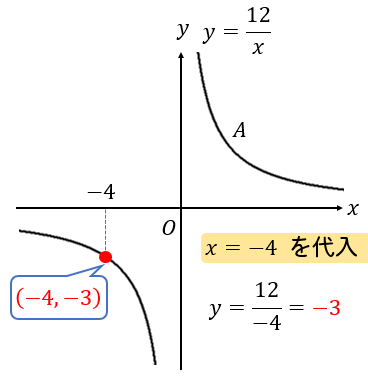
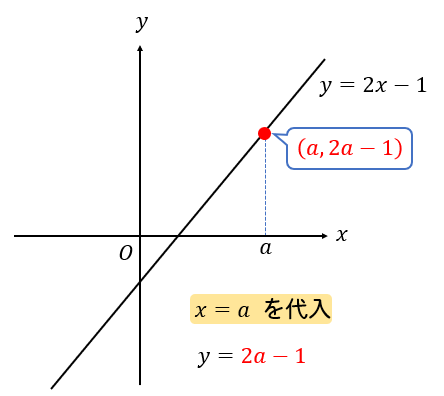
座標が文字になっていても考え方は同じですね(^^)
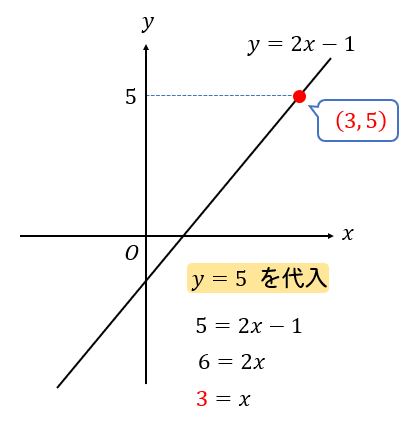
\(y\)座標が分かっている場合には、関数の式に \(y\)の値を代入して\(x\)座標を求めます。
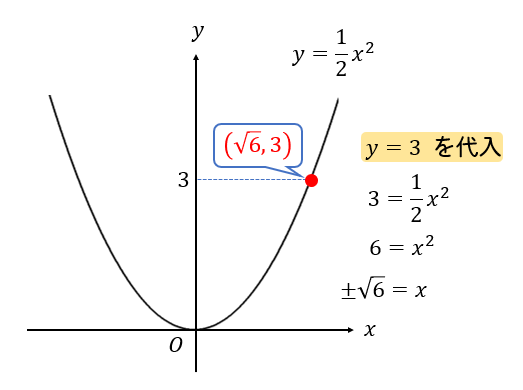
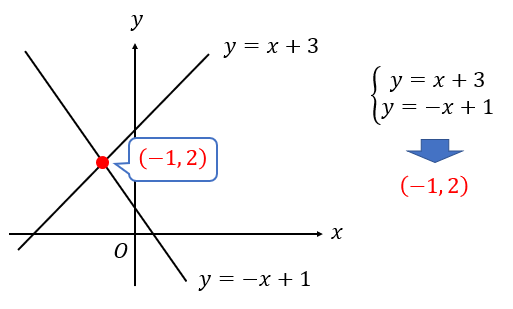
グラフの交点
グラフの交点は連立方程式で座標を求めましょう。
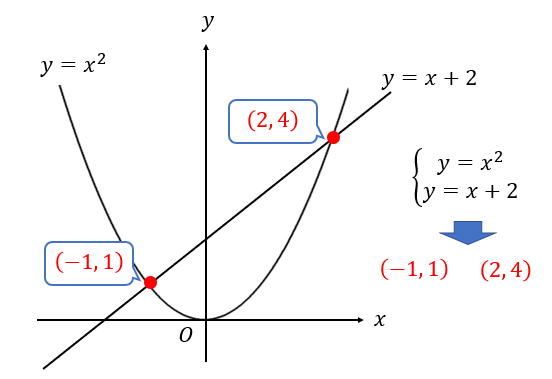
このように一次関数の利用問題で交点の座標が問われやすいです。
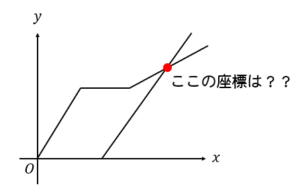
入試問題で基礎特訓!
【入試問題】
点 \((a, \ 2)\) が,1次関数\( y=\frac{1}{5}x+3 \ \)のグラフ上にあるとき,\(a\) の値を求めなさい。
点 \((a, \ 2)\) がグラフ上にあることから
\(x=a, \ y=2\) を \( y=\frac{1}{5}x+3 \ \)に代入します。
$$\begin{eqnarray}&&2=\frac{1}{5}a+3\\[5pt]&&両辺を×5する。\\[5pt]&&10=a+15\\[5pt]&&a=-5\end{eqnarray}$$
答え
$$a=-5$$
【入試問題】
下の図のように,関数 \(y=\frac{24}{x}\) とそのグラフ上の点Aを通る関数\(y=ax \)のグラフがある。点Aの\( x\)座標が6のとき,\(a\)の値を求めなさい。
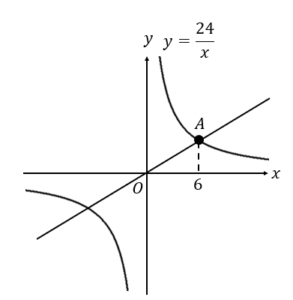
まずは点Aの座標を求めましょう。
\(x=6 \)を\( y=\frac{24}{x}\)に代入すると、
\(y=\frac{24}{6}=4\) となり、点A\((6,4)\) とわかります。
これを\(y=ax \)に代入すると\( a\)の値が求まります。
$$\begin{eqnarray}4&=&6a\\[5pt]a&=&\frac{2}{3}\end{eqnarray}$$
答え
$$a=\frac{2}{3}$$
【入試問題】
下の図で,点Cの座標を求めなさい。
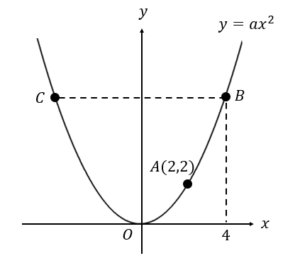
点Aの座標から\(y=ax^2 \)の比例定数を求めます。
$$\begin{eqnarray}2&=&a\times 2^2\\[5pt]2&=&4a\\[5pt]a&=&\frac{1}{2}\end{eqnarray}$$
よって、放物線の式(\(y=\frac{1}{2}x^2\)) が完成しました。
点Cの \(x\)座標は\(-4\)なので、
\(y=\frac{1}{2}\times (-4)^2=8 \)となり、点Cの座標は\( (-4, 8)\)
答え
$$(-4,8)$$
【2】長さの求め方
【動画講義】長さを求める
(動画時間:12分25秒)
長さの求め方
大きい数から小さい数をひく
横の長さなら\(x\)座標をひく。
縦の長さなら\(y\)座標をひく。
では、ポイントについて解説していきます。
次の2点ABの長さを求めなさい。
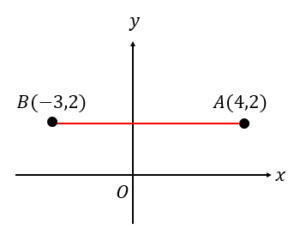
横の長さなので、それぞれの\(x\)座標の大きい方から小さい方をひきましょう。
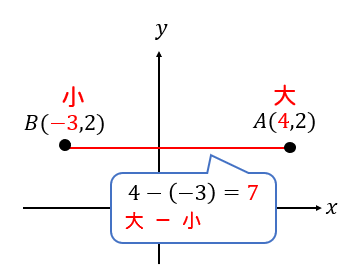
これくらい感覚で解けるよー!って方もいると思いますが、座標が文字になったときには「大ー小」の考え方が重要になります。
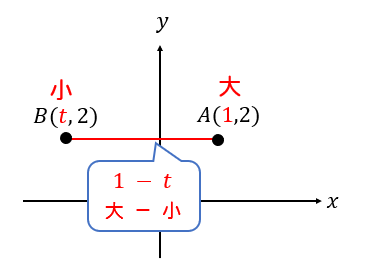
座標が文字になっても「大―小」を使えば簡単に長さが表せますね!
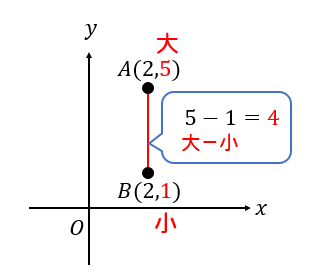
次の2点ABの長さを求めなさい。
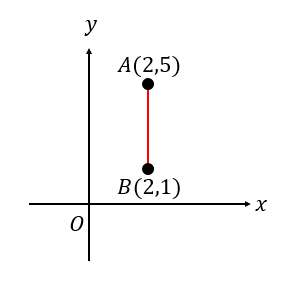
縦の長さなので、それぞれの\(y\)座標の大きい方から小さい方をひきましょう。
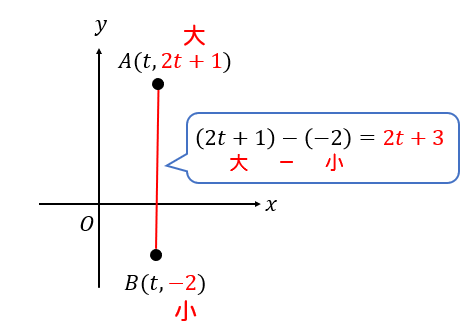
こちらも座標が文字になっても考え方は同じですね!
三平方の定理を用いた距離

次の2点ABの距離を求めなさい。
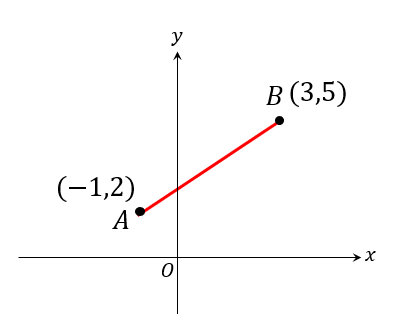
このように斜めになっている長さは三平方の定理を使って次のように求めます。
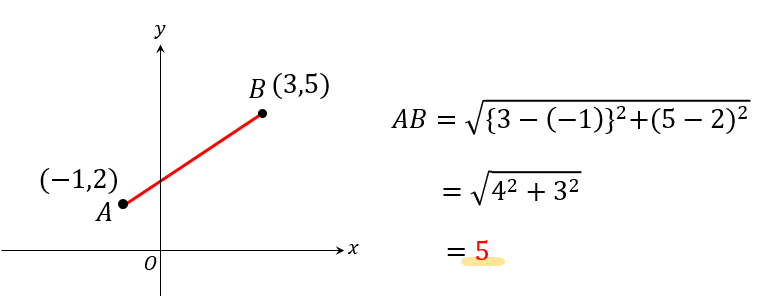
三平方の定理がどんなものだったかも含めて、こちらの記事で詳しく解説しているので参考にしてみてください。
演習問題で完全理解!
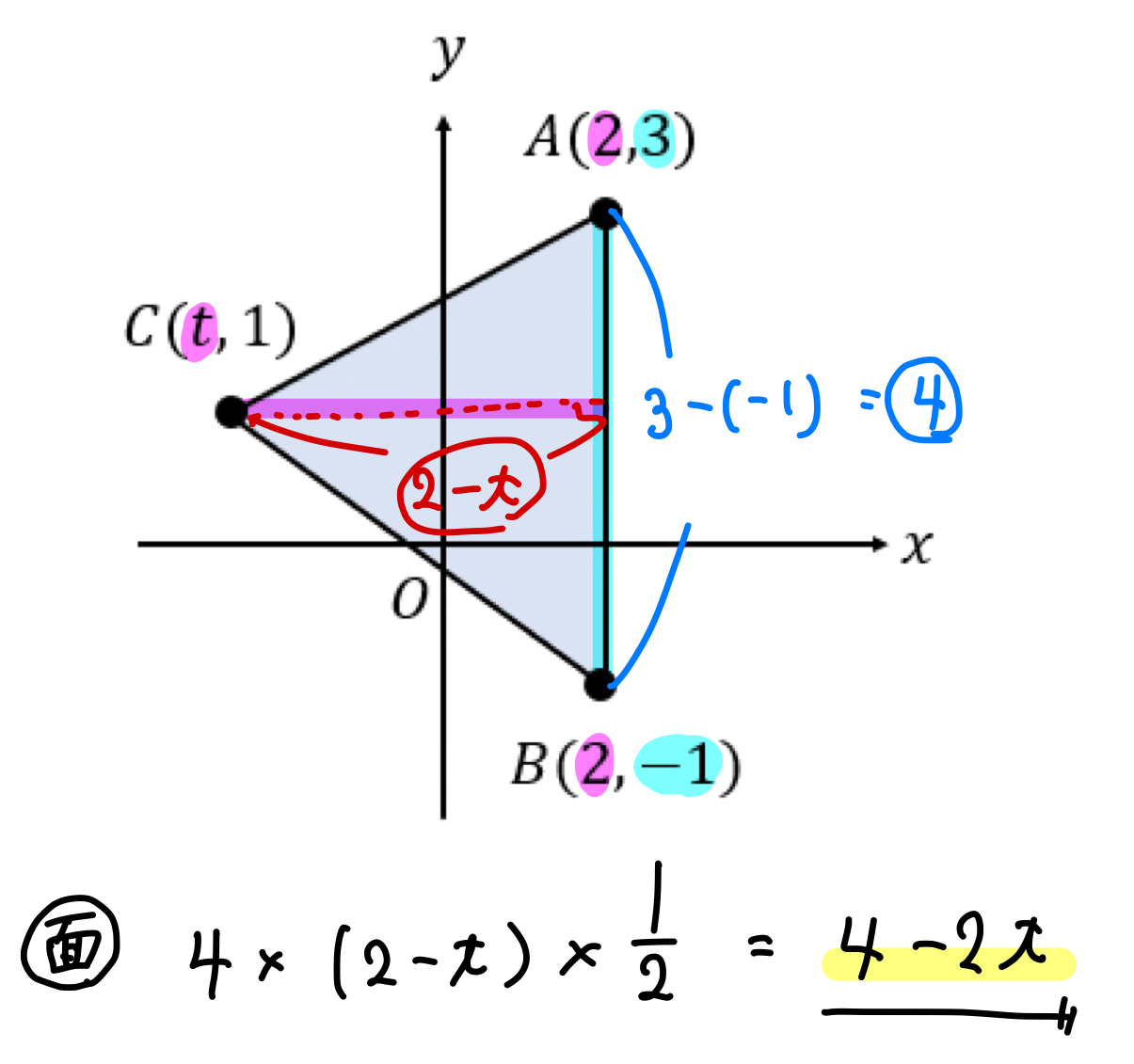
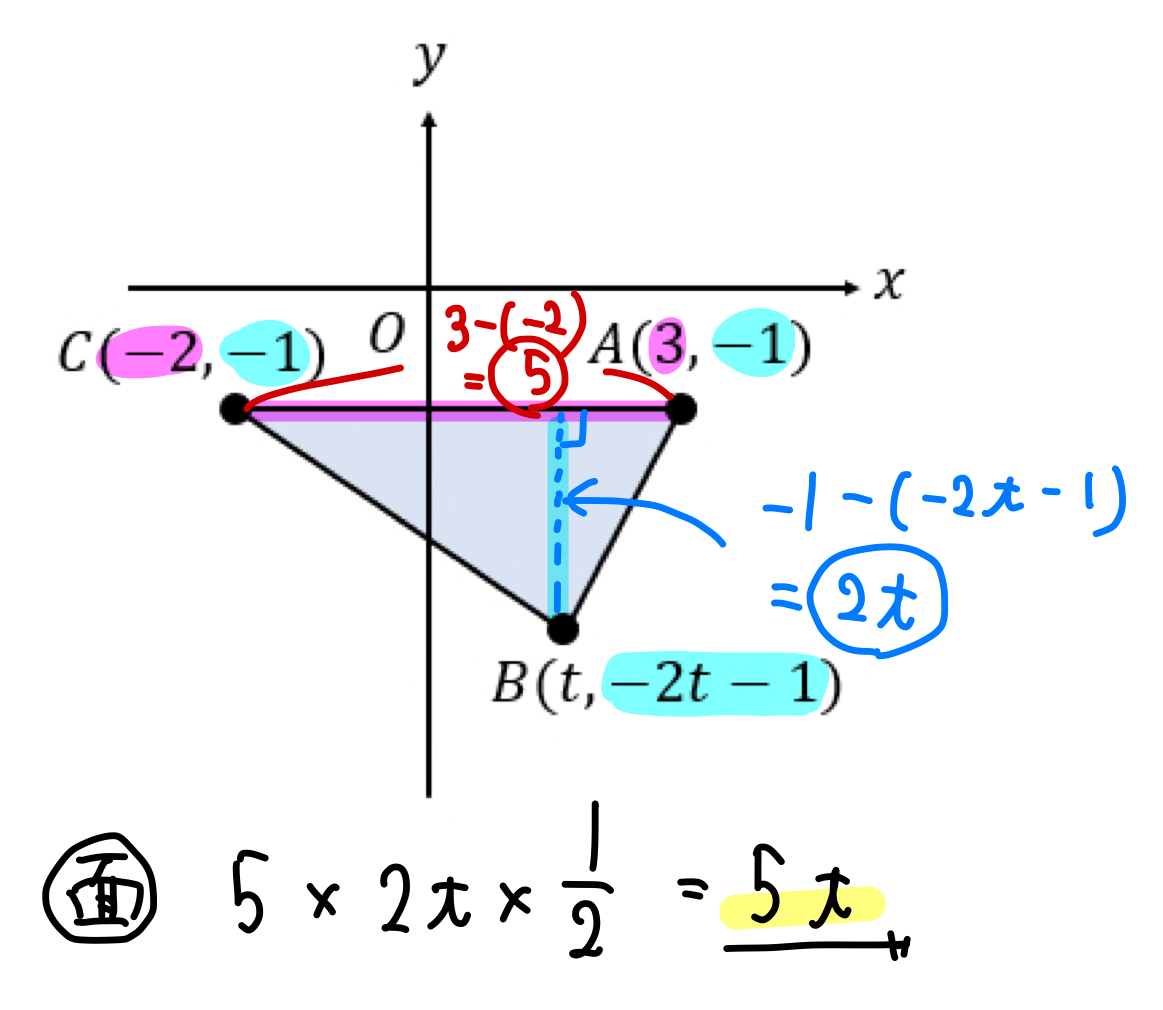
次のグラフにおいて,△ABCの面積を文字で表しなさい。
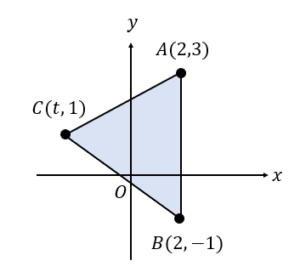
次のグラフにおいて,△ABCの面積を文字で表しなさい。
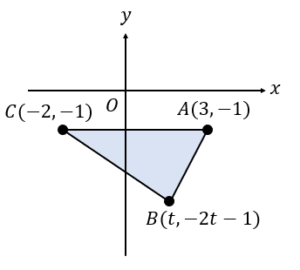
【3】文字座標の応用
「座標、長さ」について理解を深めてもらったところで、文字座標の応用に挑戦してみましょう!
まずは問題に挑戦してみてください。
その上で動画解説を見て要点をチェック、理解を深めてください。
演習問題①

座標を文字で置いて考えることがポイントです。
文字を使って面積を表す ⇒ 方程式を作って解く。
この流れが王道ですので、たくさん演習をこなして慣れていきましょう。
座標を文字で置く場合には、\(x\)座標を\(t\)でおく。その座標を通るグラフの式に \(x=t\) を代入して \(y\)座標を表しましょう。
演習問題②

台形の面積はバッチリでしたか??
関数の面積では台形が問われることも多いので覚えておきましょう。
台形の面積
$$\{(上底)+(下底)\}\times (高さ)\times \frac{1}{2}$$
追加受講プレゼント!
お疲れさまでした!
今回の講義をすべて終えたら
- この講座に期待すること
- あなたが勉強で困っていること
- 今回の講義の感想、質問
- あなたの意気込み
これらを下のコメント欄に書き込んでください。
コメントは承認制となっているので、
記事に公開されるまでに時間がかかります。
こちらでコメントを確認後、
ご記入いただいたメールアドレス宛に
通常1~3日以内に追加講義を送らせていただきます。
ご記入いただいたメールアドレスは公開されないのでご安心くださいね!
コメントはこちらから
↓ ↓ ↓ ↓ ↓
受講させていただきました。
今回の問題は理解して解けましたが、初見の応用問題だとなかなか自力で解けません。
いろいろ問題を解いて頑張ります。
ありがとうございました。
受講お疲れさまでした!
>今回の問題は理解して解けました
素晴らしいです!
まずは1つずつ理解していくことが大事です。
今回の内容が理解できたなら、
確実に成長できているので自信を持ってくださいね。
>初見の応用問題だとなかなか自力で解けません。
>いろいろ問題を解いて頑張ります。
ここは経験を積んでいくほかありません。
みんさんがおっしゃっているように
たくさん問題を解いてがんばっていきましょう!
たくさん問題を解くときに、
今回学んだ「座標」「長さ」の知識が
必ず生きてくると思いますよ。
ファイトです!