【問題】
下の図のように、関数\(y=-\frac{1}{3}x+4\) のグラフ上に点\((3,3)\) があり、このグラフと\(y \)軸との交点をBとします。また、関数\(y=-\frac{1}{3}x\) のグラフ上を\(x<0 \)の範囲で動く点C、\(y \)軸上に点D\((0,3)\)があります。
（1）四角形ABCOが平行四辺形となるとき、点Cの座標を求めなさい。
（2）点Dを通り、△ABOの面積を2等分する直線の式を求めなさい。
解答
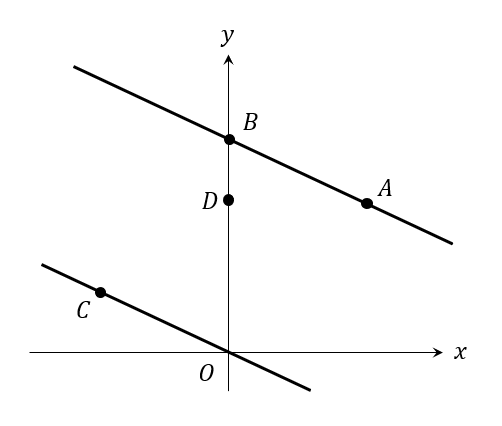
答え
（1）\((-3,1)\)
（2）\(y=-\frac{1}{2}x+3\)
解説
（1）
平行四辺形の対辺は、平行で辺の長さが等しくなります。
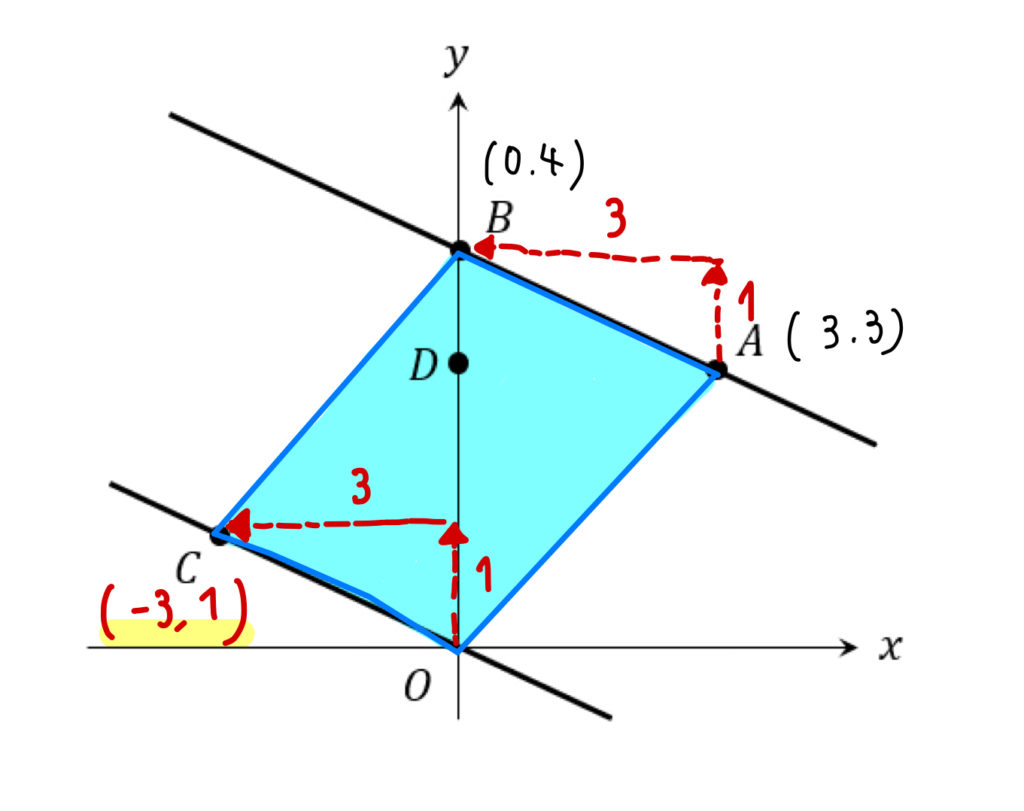
なので、このように座標の変化も等しくなります。
（2）
まず、△ABOの面積を求めると6になることが分かります。
つまり、△ABOを二等分すると面積が3の図形に分けられることになります。
点Dを通る△ABOを二等分する線を赤線として
イメージ図を書くとこんな感じになります。
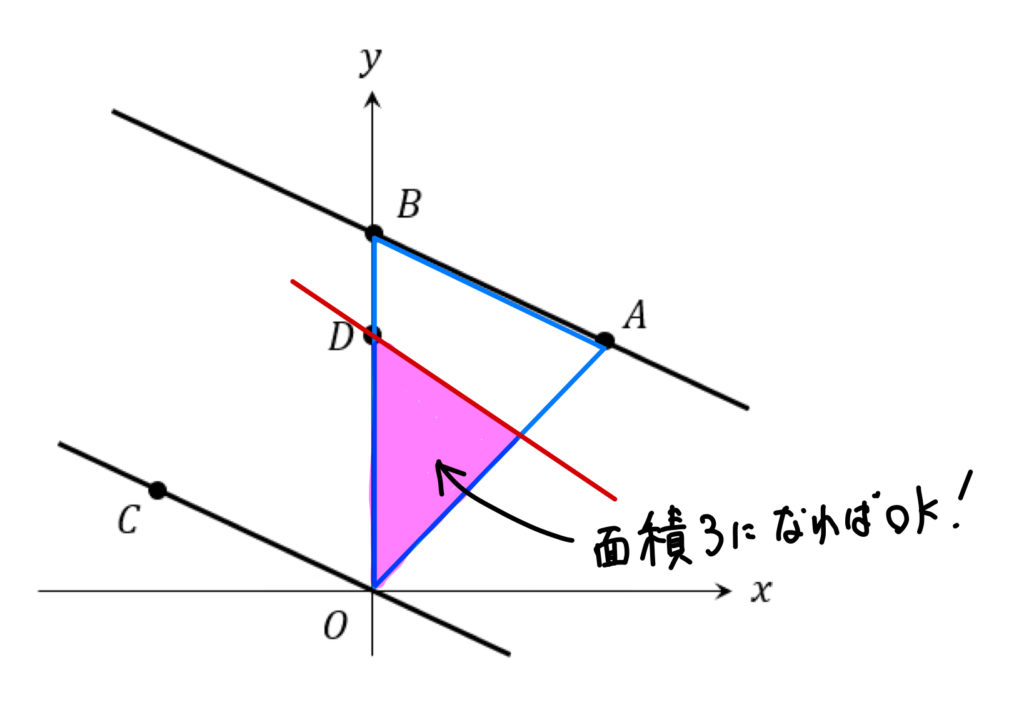
つまり、この赤い部分の面積が3になっていればOKということですね。
この赤線と直線OA（\(y=x\)）の交点をPとして、
その\(x\)座標を\(a \)とすると、P\((a,a)\)と表せます。
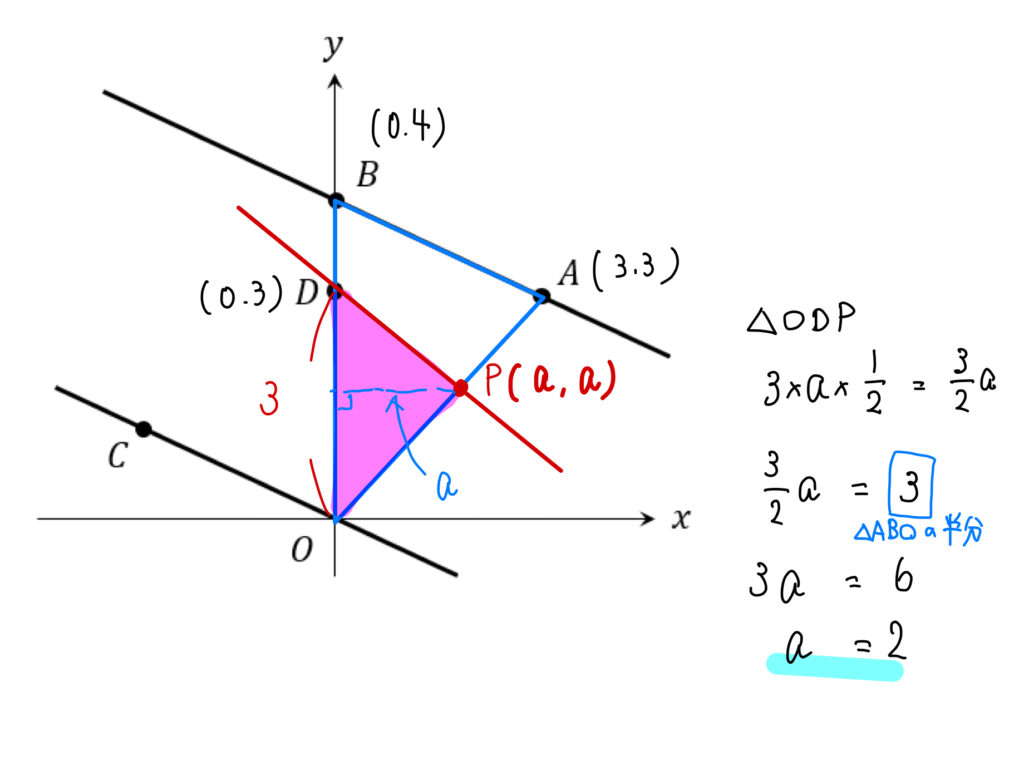
△ODPの面積が3になることから、\(a=2\)になると分かります。
つまり、△ABOを二等分する直線は、
2点D\((0,3)\)、P\((2,2)\)を通るということなので、
\(y=ax+b\)に当てはめて計算をしていくと、\(y=-\frac{1}{2}x+3\)となります。