【埼玉16】関数の入試問題（★★☆）

【問題】

下の図で、曲線は関数\(y=\frac{1}{2}x^2 \)のグラフです。曲線上に\(x \)座標が\(-1\)、\(3\)である2点A、Bをとります。

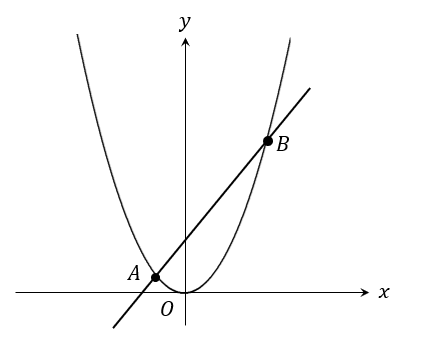
（1）直線ABの式を求めなさい。

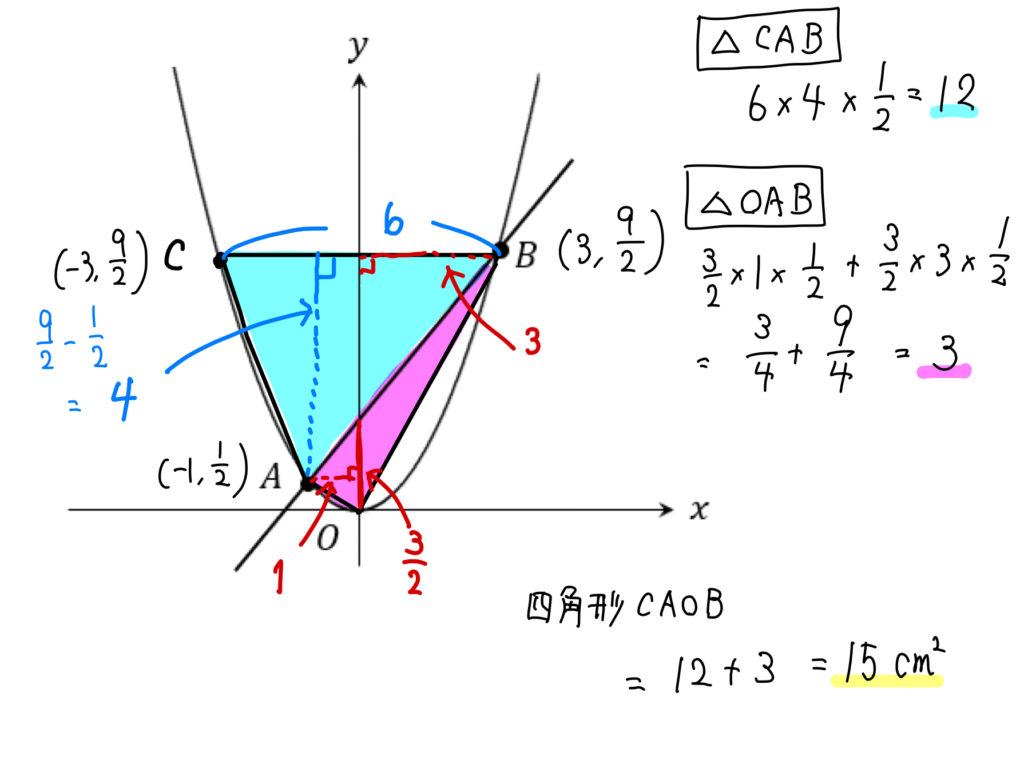
（2）\(y\)軸を対称の軸として点Bと線対称である点Cをとり、四角形CAOBをつくります。この四角形CAOBの面積を求めなさい。

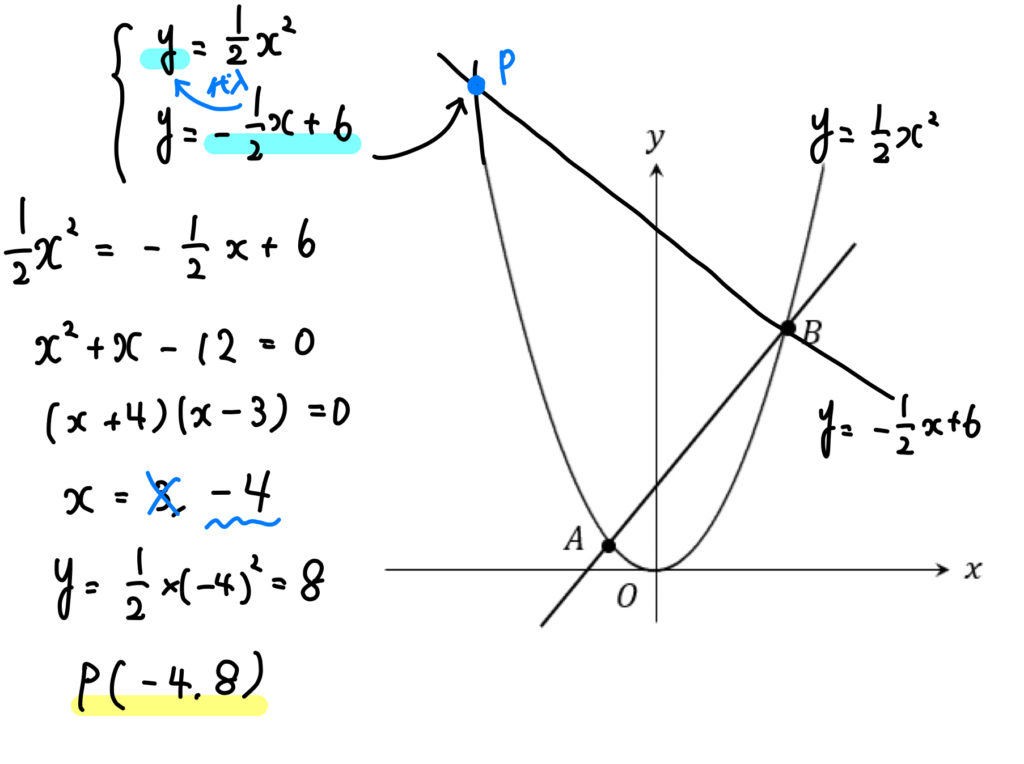
（3）曲線上を、\(x\)座標が\(x<-1 \)の範囲で動く点Pを考えます。△PABと△POBの面積が等しくなるとき、点Pの座標を求めなさい。

絶対合格！

関数完全攻略セミナー

塾は不要！家にいながら本格的な学びができる

基礎が身につく6つのステップ

入試に出る14パターン

動画を見るだけで解けるようになる！

《講義内容》

「基礎が身につく6つのステップ」

1. 関数の式のつくり方　（29分57秒）
2. グラフのかき方　（10分45秒）
3. 変域の求め方　（16分07秒）
4. 変化の割合　（12分39秒）
5. 座標の求め方　（23分18秒）
6. 長さの求め方　（12分25秒）

「基礎定着演習」

• 6つのステップを実践で活かす演習（18分52秒）
• 基礎定着問題集　97問

【応用力を高める発展演習】

グラフの面積を求める

• 放物線と直線の面積（7分57秒）
• 全体から取り除く面積（5分23秒）
• 面積の比を求める（5分43秒）

三角形の面積を2等分

• 2等分はどこを通る？（5分55秒）
• 面積を2等分する直線（6分27秒）

相似を利用、座標⇔比の考え方

• 座標⇔比の基本的な考え方（7分23秒）
• AC:AB＝3:4の座標は？（5分14秒）

座標を文字で置いて考える

• 文字座標で面積を表す（9分58秒）
• 台形の面積を2等分（7分00秒）
• 双曲線と放物線の組み合わせ（7分23秒）
• 面積が等しくなるのは？（6分09秒）
• y座標から文字で表す方法（11分24秒）
• 四角形の面積はこうやって考える（5分43秒）
• 傾きをヒントに座標を求める（6分11秒）

放物線と四角形

• 正方形になるのは？（8分39秒）
• 四角形の面積の2/5倍（7分09秒）

最短距離

• 長さの和が最短になる考え方（4分56秒）
• 放物線と最短距離（2分22秒）
• 双曲線と最短距離（2分28秒）

等積変形

• 等積変形の考え方、基本演習（6分27秒）
• 四角形⇒三角形への等積変形（6分29秒）
• x軸上に点をとって等積変形（3分59秒）
• 等積変形って気づける？（6分44秒）

平行四辺形

• 平行四辺形になる座標、面積の2等分（6分55秒）
• 面積の2等分は対角線が大事！（4分39秒）
• 平行四辺形の面積はこうやるべし！（9分52秒）
• 変化量から座標を求める（8分41秒）

動点

• 動点の基礎講義～一次関数～（15分50秒）
• 動点の基礎講義～2次関数～（16分02秒）
• 動点と三角形、どんなグラフ？（12分12秒）
• 二等辺三角形になるのは何秒後？（10分39秒）
• 動点の長さを求めるワザ（10分45秒）
• 図形が動いていく問題（8分45秒）

グラフの利用（速さ）

• 追いつくパターンの基礎講義（15分21秒）
• 途中で速さが変わる（8分16秒）
• バスの往復、すれ違うのは？（11分12秒）
• 往復する兄と弟、それぞれ速さは？（9分45秒）
• 放物線と直線の組み合わせ（11分54秒）

グラフの利用（水そう）

• 2つの水そうの変化（8分40秒）
• 水そうのおもりと体積（6分38秒）
• 排水と給水、1分間の変化は？（6分40秒）

グラフの利用（その他）

• ろうそくが燃えつきるのは？（9分05秒）
• 電気料金、式で表せる？（7分49秒）

格子点

• 格子点の数え方は？（6分53秒）
• 格子点の実践編（7分56秒）
• 格子点と線分の関係（4分58秒）

回転体の体積

• 回転体は楽して式を作れ！（6分40秒）
• 円錐が空洞になってるパターン（3分39秒）
• 辺が斜めになっているなら？（5分05秒）
• 直角三角形になるには？（7分16秒）
• 激ムズ回転体の考え方とは（5分14秒）