【問題】
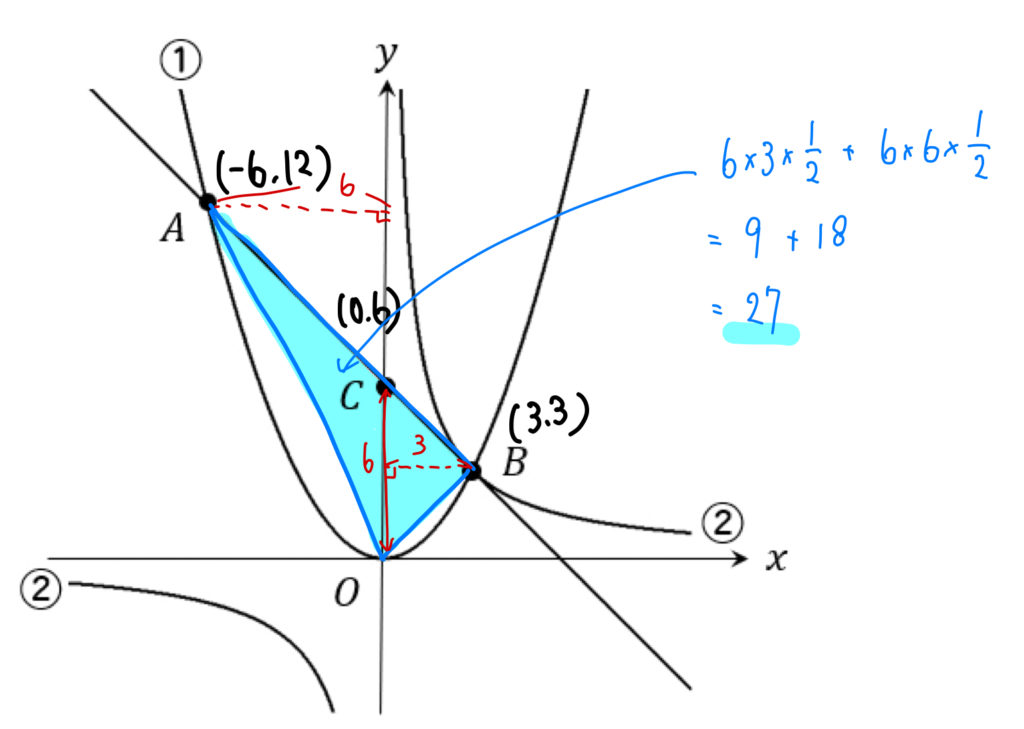
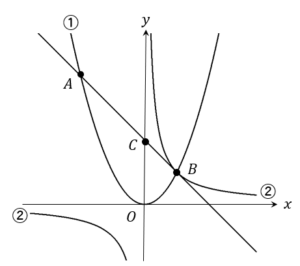
下の図において、①は関数\(y=\frac{1}{3}x^2\) のグラフで、②は反比例のグラフである。①と②は点Bで交わっていて、点Bの\(x\) 座標は3である。また、①のグラフ上に\(x\) 座標が\(-6\) である点Aをとり、直線ABと\(y\) 軸との交点をCとする。
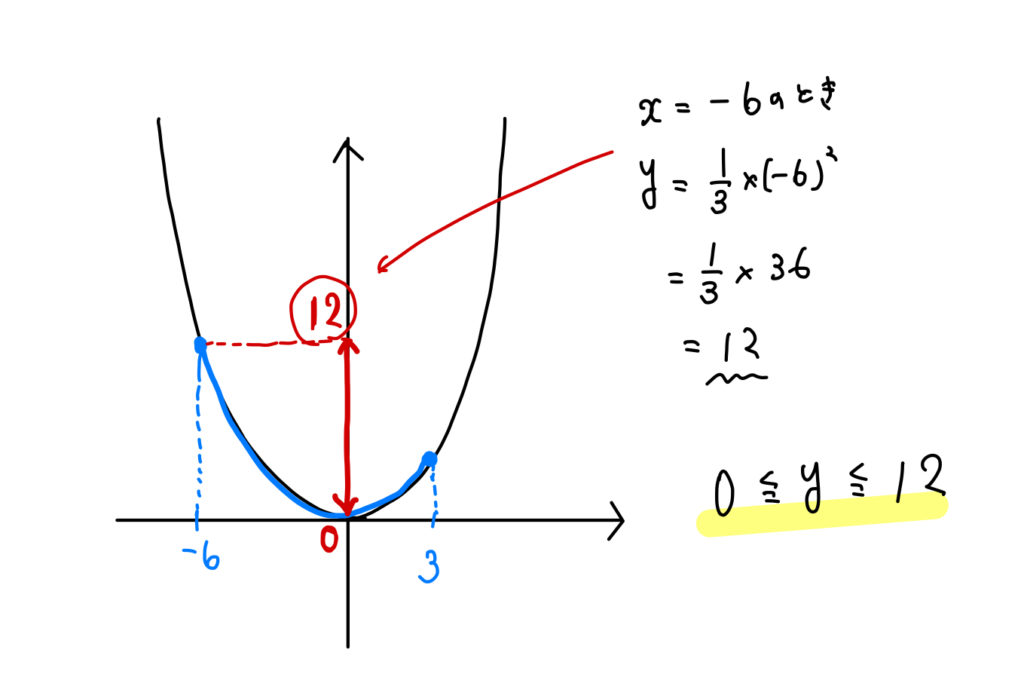
（1）関数\(y=\frac{1}{3}x^2\) について、\(x\) の変域が\(-6≦x≦3\) のときの\(y \)の変域を求めなさい。
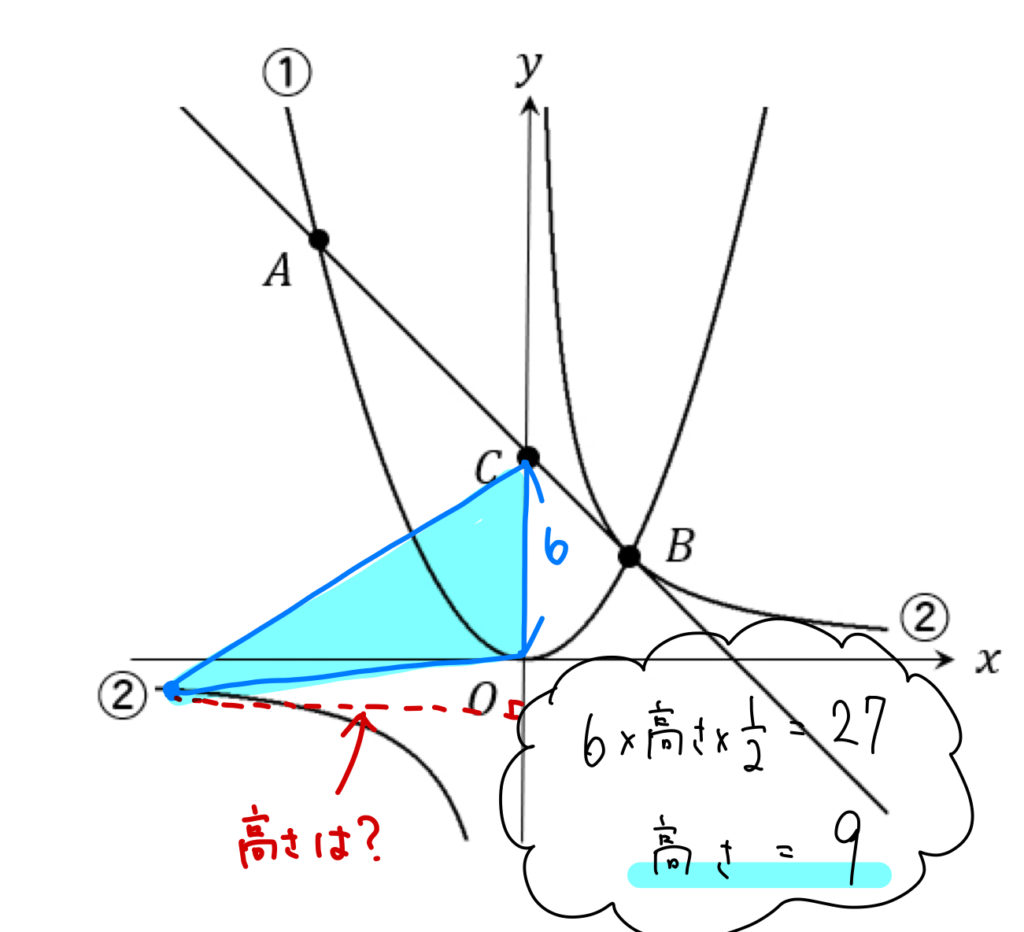
（2）②のグラフ上に\(x\) 座標が負である点Pをとる。△OABと△OCPの面積が等しくなるとき、点Pの座標を求めなさい。
解答
答え
（1）\(0≦y≦12\)
（2）\((-9,-1)\)
解説
（1）
（2）
まずは△OABの面積を求めましょう。
そのためには、直線ABの式、頂点B、Cの座標を求める必要があります。
すると、△OABの面積を次のように求めることができます。
となると、△COPの面積を27にするためには、
線分COを底辺と考えた場合、
高さを9にする必要があります。
つまり、点Pの\(x\)座標は\(-9\)であることがわかります。
②の反比例の式は、\((3,3)\)を通ることから\(y=\frac{9}{x}\)。
この式に、\(x=-9\)を代入すると、\(y=-1\)。
よって、点Pの座標は\((-9,-1)\)となります。