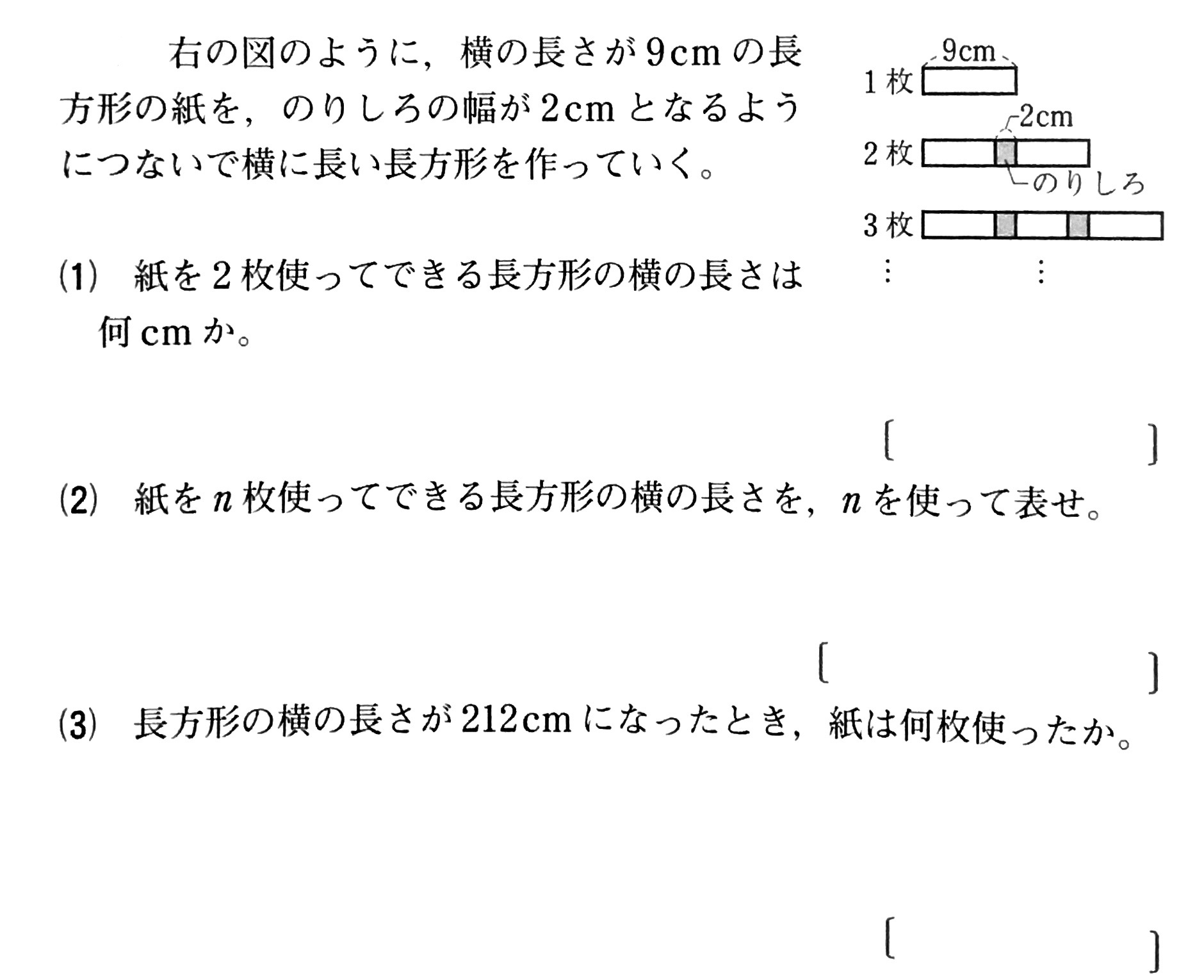
解答
答え
(1)\(16㎝\)
(2)\((7n+2)cm\)
(3)\(30枚\)
(1)の解説
1枚のときより、何㎝分増えているのか注目しましょう。
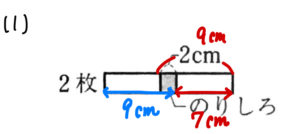
すると、このように7㎝分だけ増えていることが分かりますね。
よって、\(9+7=16\)cmとなります。
このことから、今回の問題では、
1枚増やすごとに横の長さは7㎝ずつ増えていくということが読み取れます。
(2)の解説
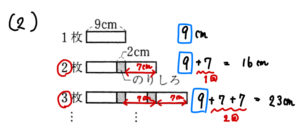
1枚のとき、\(9cm\)
2枚のとき、\(9+7=16cm\)
3枚のとき、\(9+(7+7)=23cm\)
と表すことができます。
2枚のときには、7が1回加えられている。
3枚のときには、7が2回加えられている。
10枚のときには、7は9回加えられるはず。
つまり、長方形の枚数から1を引いた数だけ
7が加えられるという規則性に気が付くはずです。
では、\(n\)枚のときには?
となると、\((n-1)\)回加えられるはずですよね。
よって、長方形を\(n\)枚並べたときの横の長さは
$$9+7\times(n-1)=(7n+2)㎝$$
となります。
決まった数だけ増えたり、減ったりする数列のことを等差数列といいます。
このとき、\(n\)番目の式は次のように表せます。
$$(最初の数)+(n-1)\times (増減する数)$$
今回の問題では、これに当てはめると
$$9+(n-1)\times 7=7n+2$$
と表すことができます。
(3)の解説
(2)で作った\(n\)の式を利用すれば簡単です。
$$\begin{eqnarray}7n+2&=&212\\[5pt]7n&=&210\\[5pt]n&=&30 \end{eqnarray}$$
よって、答えは30枚となります。