【問題】
下の図において、アは関数y=\frac{1}{4}x^2、イは関数y=x^2のグラフであり、点Aはア上の点でx 座標が正である。点Aを通りy 軸に平行な直線とイの交点をBとする。点Bを通り、x 軸に平行な直線とイの交点のうち、x 座標が負である点をCとし、点Cを通りy 軸に平行な直線とアの交点をDとする。
（1）点Aのx 座標が4のとき、点Cの座標を求めなさい。
（2）四角形ABCDが正方形であるとき、点Aのx座標を求めなさい。
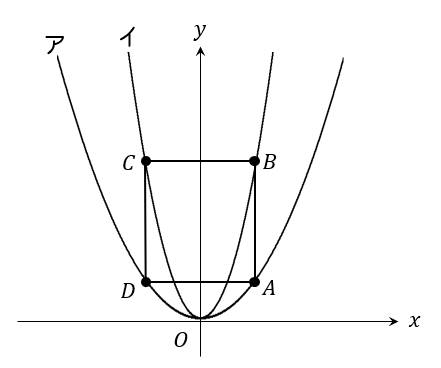
答え
（1）C(-4,16)
（2）\frac{8}{3}
（1）
点Aの座標 ⇒ 点Bの座標 ⇒ 点Cの座標
このようにたどっていきましょう。
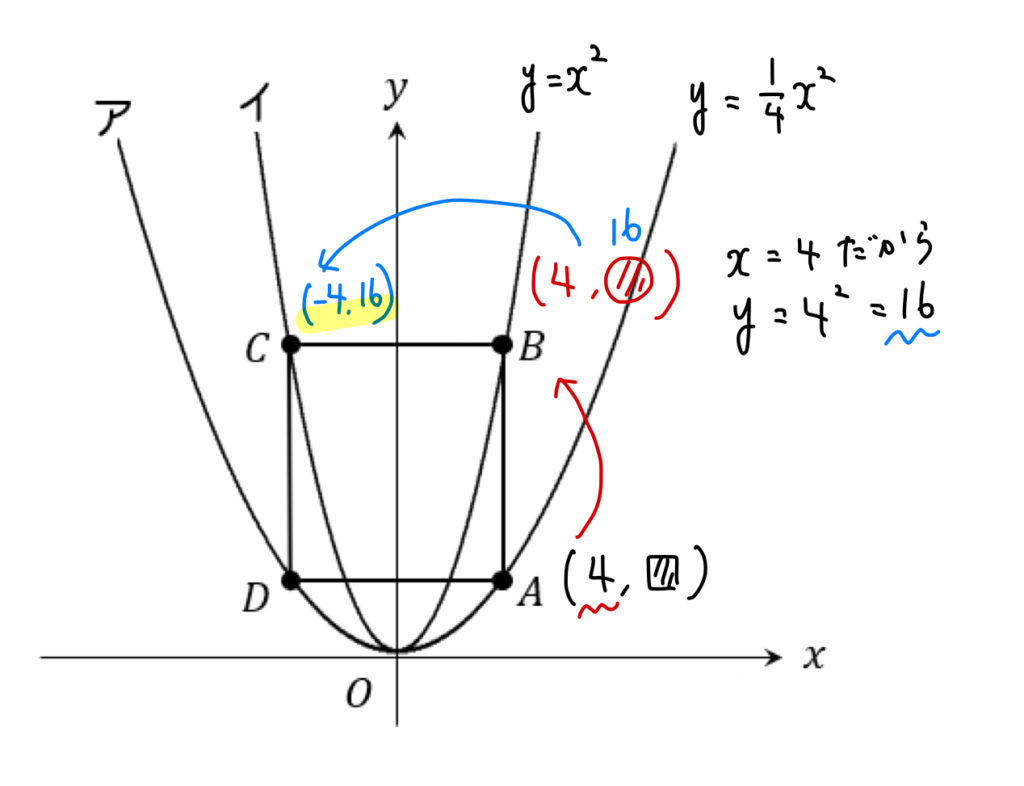
点Aのx座標が4だから、
真上にある点Bのx座標も4になる。
すると、点Bはy=x^2上の点だから、
x=4を代入すると、y=4^2=16となります。
点Cは、点Bをy軸に対して折り返したところにある点なので、
x座標の符号をチェンジして、
点B(4,16) ⇒ 点C(-4,16)
とすることができます。
（2）
正方形ということは、すべての辺が等しくなるはずです。
というわけで、辺AB、辺ADを文字で表し、
それらの長さが等しくなるということで
方程式を作っていきましょう。
点Aのx座標をaとすると、次のように表すことができます。
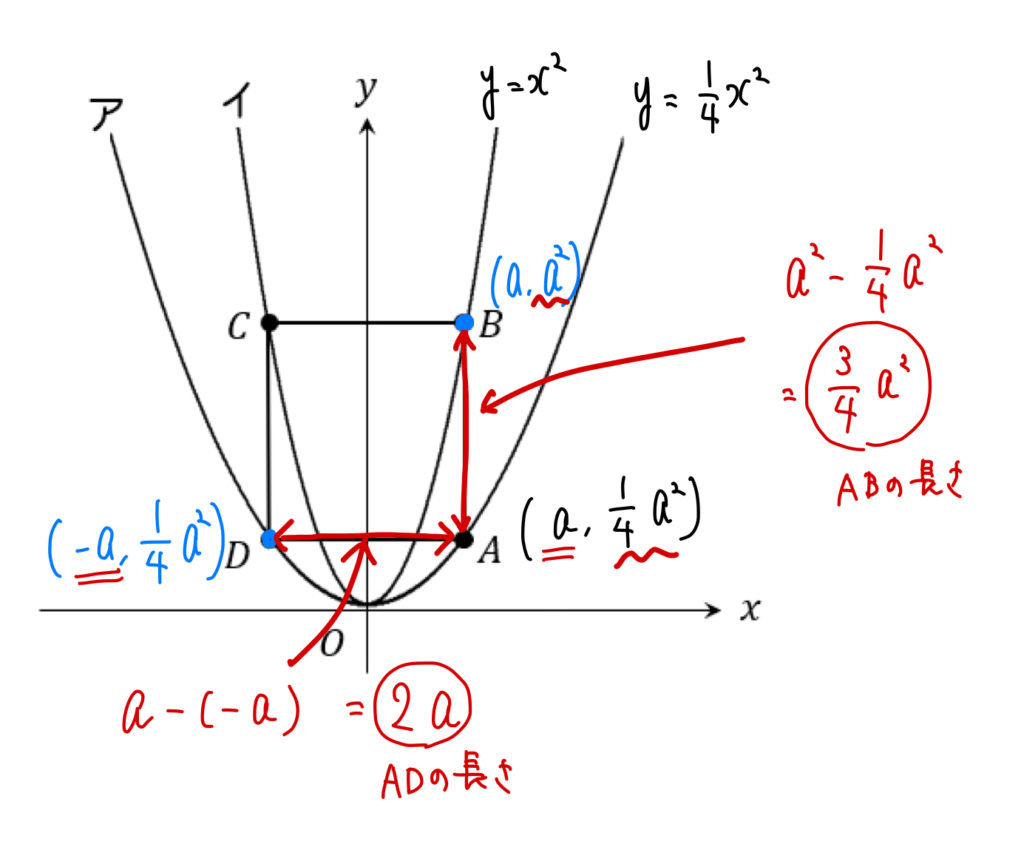
座標が求まれば、上のようにそれぞれの長さも求めれますね。
縦の長さを求める場合は、y座標を引く。
横の長さを求める場合は、x座標を引けばよいです。
では、辺AB、辺ADの長さが等しくなれば正方形になるので…
\begin{eqnarray}\frac{3}{4}a^2&=&2a\\[5pt]3a^2&=&8a\\[5pt]3a^2-8a&=&0\\[5pt]a(3a-8)&=&0\\[5pt]a&=&0,\frac{8}{3}\end{eqnarray}
a=0のときは、点Aが原点になってしまって正方形が作れなくなるので問題に合いません。
よって、答えはa=\frac{8}{3}